Propriétés topologiques
Les intervalles de \(\mathbb R\) jouent un rôle fondamental dans l'étude des fonctions numériques (fonctions de \(\mathbb R\) vers \(\mathbb R\)), tant du point de vue global (ensemble de définition) que local (voisinage): ce sont les parties connexes, c'est à dire d'un seul tenant, de \(\mathbb R\).
Définition :
Une partie \(I\) de \(\mathbb R\) est un intervalle si
\(\forall a, b \in I ,a \leq b, \forall x \in \mathbb R ,(a\leq x \leq b \Rightarrow x\in I)\).
La propriété de la borne supérieure (resp. inférieure) permet de classer les intervalles non vides de \(\mathbb R\) en 9 types distincts suivant l'existence ou non d'un majorant, d'un minorant, d'un plus grand, d'un plus petit élément.
On montre ainsi qu'un intervalle non vide de \(\mathbb R\) est d'un des types suivants :
Explication :
intervalle borné :
ouvert : \(]a,b[=\{x\in\mathbb R, a<x<b\}\)
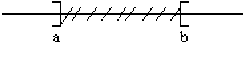
semi-ouvert :
\([a,b[=\{x\in\mathbb R, a\leq x<b\}\)
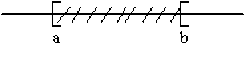
\(]a,b]=\{x\in\mathbb R, a<x\leq b\}\)
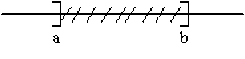
fermé : \([a,b]=\{x\in\mathbb R, a\leq x\leq b\}\)
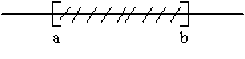
intervalle non borné :
minoré, non majoré :
avec minimum \([a,+\infty[=\{x\in \mathbb R, x\geq a\}\)
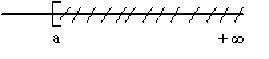
sans minimum \(]a,+\infty[=\{x\in \mathbb R, x>a\}\)
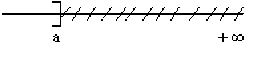
majoré, non minoré :
avec maximum \(]-\infty,b]=\{x\in\mathbb R, x\leq b\}\)
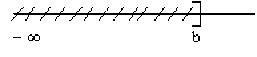
sans maximum \(]-\infty,b[=\{x\in\mathbb R, x<b\}\)
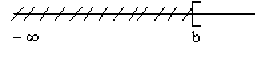
non minoré, non majoré : \(]-\infty, +\infty[\)
Par exemple, on peut montrer qu'un intervalle borné ayant un plus petit élément mais pas de plus grand élément est de la forme \([a,b[\).
Preuve :
Soit \(I\) un tel intervalle, \(a\) son plus petit élément, \(b\) sa borne supérieure, alors
tout réel \(x\) vérifiant \(x< a\) n'appartient pas à \(I\),
tout réel \(x\) vérifiant \(x\geq b\) n'appartient pas à \(I\),
l'intervalle \(I\) est inclus dans \([a,b[\), et tout \(x\) de \([a,b[\) appartient à \(I\).
Les intervalles \(]a,b[\) et \([a,b]\), (\(b>a\)) peuvent être encore définis de la façon suivante :
\(]a,b[=\{x\in\mathbb R, \|x-\frac{a+b}{2}\|<\frac{b-a}{2}\}\)
\([a,b]=\{x\in\mathbb R, \|x-\frac{a+b}{2}\|\leq\frac{b-a}{2}\}\)
Le réel \(\frac{a+b}{2}\) est le centre de l'intervalle, \(\frac{b-a}{2}\) est le rayon. Cette définition de l'intervalle \(]a,b[\), sera très souvent utilisée, en particulier, dans l'étude des suites et des fonctions.
Les propriétés locales font appel à la notion de voisinage d'un point.
Définition :
Soit \(a\in\mathbb R\), on dit que \(a\) est intérieur à un intervalle \(I\) s'il existe un intervalle ouvert contenant \(a\) et inclus dans \(I\). On appelle voisinage de \(a\) toute partie de \(\mathbb R\) qui contient un intervalle ouvert contenant \(a\). On appelle voisinage de \(+\infty \)(resp. \(-\infty\)) toute partie de \(\mathbb R\) qui contient un intervalle de la forme \(]A,+\infty[\) avec \(A\in\mathbb R\), (resp.\(]-\infty,B[\) avec \(B\in\mathbb R\)). On dit qu'une propriété est réalisée au voisinage d'un point s'il existe un voisinage du point dans lequel cette propriété est vérifiée .
Pratiquement on prendra pour voisinage de \(a\in\mathbb R\), les intervalles ouverts contenant \(a\) (fréquemment les intervalles ouverts centrés en \(a\) ) et pour voisinage de \(+\infty\) (resp. \(-\infty\)) les intervalles \(]A,+\infty[\), (resp. \(]-\infty,B[\)).
Si \(V\) est un voisinage de \(a\), on note \(V^* =V-\{a\}\), voisinage épointé de a .
Théorème :
\(\mathbb Q\) est dense dans \(\mathbb R\).
(entre deux nombres réels distincts \(a\) et \(b\), il existe un rationnel)
Preuve :
Ceci peut être démontré en utilisant une approximation décimale de \(\frac{a+b}{2}\).
Soient \(a\) et \(b\) deux réels, vérifiant \(a<b\); on pose \(l=b-a>0\),
si \(\frac{a+b}{2}\) est rationnel, il convient car il vérifie \(a <\frac{a+b}{2}< b\),
si \(\frac{a+b}{2}\) n'est pas rationnel, soit \(k\in\mathbb N\) tel que \(10^{-k}<l/2\); le réel \(\frac{a+b}{2}\) admet une approximation décimale à \(10^{-k}\) près par défaut \(x_{k}\) et l'on a : \(a<x_{k}<\frac{a+b}{2}< b\), avec \(x_k\in\mathbb D\).
Le rationnel \(x_k\) convient donc.
On montre de même que \(\mathbb R \)\ \(\mathbb Q\) (ensemble des nombres irrationnels) est dense dans \(\mathbb R\).