Cas où l'exposant est un entier strictement négatif
Soit \(n\) un entier strictement négatif, on pose \(n = - p\) avec \(p\) entier strictement positif.
Pour tout réel \(x\) non nul on a : \(x^n = x^{-p} = \frac{1}{x^p}.\)
L'étude de la fonction \(f~~x \mapsto x^n\) peut donc se déduire de celle de \(g~~x \mapsto x^p\) faite précédemment.
La fonction \(g\) est définie et continue sur \(\mathbb R,\) nulle pour \(x = 0,\) donc \(f = \frac{1}{g}\)est définie et continue sur \(\mathbb R ^*.\)
Comme la fonction \(g, f\) est paire ou impaire suivant que \(n\) est pair ou impair.
La fonction \(g\) étant positive, strictement croissante sur \(]0, +\infty[,\) la fonction \(f\) est strictement décroissante sur le même intervalle.
On a les limites suivantes :
\(\displaystyle \lim_{x \rightarrow +\infty} x^n = \displaystyle \lim_{x \rightarrow +\infty} \frac{1}{x^p} = 0~\textrm{et}~\displaystyle \lim_{x \rightarrow -\infty} x^n = \displaystyle \lim_{x \rightarrow -\infty} \frac{1}{x^p} = 0\)
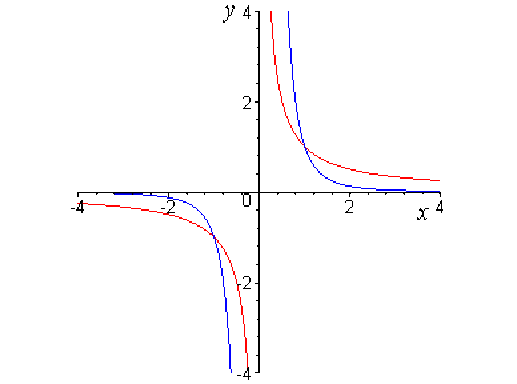
\(\displaystyle \lim_{x \rightarrow 0, x > 0} x^n = \displaystyle \lim_{x \rightarrow 0, x > 0} \frac{1}{x^p} = +\infty\)
et, selon la parité, \(\displaystyle \lim_{x \rightarrow 0, x < 0}x^n = +\infty\) (\(n\) pair), \(\displaystyle \lim_{x \rightarrow 0, x < 0}x^n = -\infty\)(\(n\) impair).
La représentation graphique de la fonction \(f\) admet donc deux asymptotes : l'axe \(x'x\) et l'axe \(y'y.\)
La fonction \(g\) est dérivable sur \(\mathbb R,\) donc \(f = \frac{1}{g}\) est dérivable sur \(\mathbb R ^*.\)
Pour tout réel \(x\) non nul on a : \(f'(x) = \frac{-g'(x)}{(g(x))^2}.\)
Or \(g'(x) = px^{p-1}\)
D'où, en utilisant les propriétés des exposants entiers \(f'(x) = \frac{-px^{p-1}}{(x^p)^2} = -p\frac{x^{p - 1}}{x^{2p}} = -px^{-p-1}.\)
La dérivée de \(x \mapsto x^n\)pour \(n \in \mathbb Z ^{*-}\)est donc \(x \mapsto nx^{n-1},\) formule identique à celle obtenue pour \(n \in \mathbb Z ^{*+}.\)
D'où les tableaux de variations selon la parité de \(n\) :
Cas où \(n\) est pair
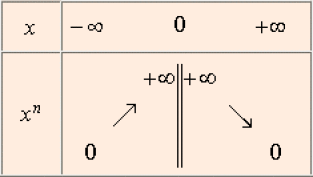
Cas où \(n\) est impair
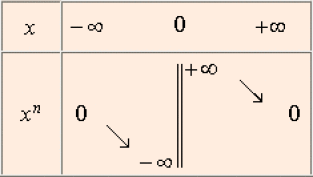
Voici, dans un repère orthonormé, quelques exemples de graphes :
Cas où \(n\) est pair
\(\color{red} x \mapsto x^{-2}\)
\(\color{blue} x \mapsto x^{-4}\)
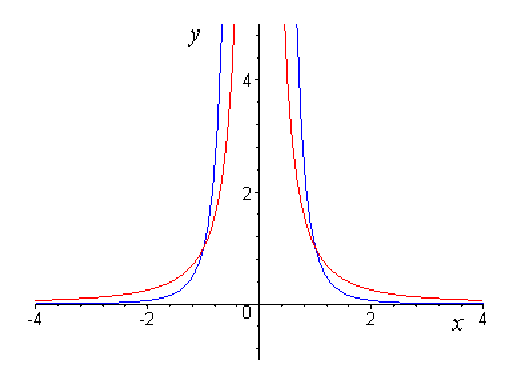
Cas où \(n\) est impair
\(\color{red} x \mapsto x^{-1}\)
\(\color{blue} x \mapsto x^{-3}\)