Fonction Arcsinus
Définition :
Soit \(f\) la restriction de la fonction sinus à l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}].\)
\(f :[-\frac{\pi}{2}, \frac{\pi}{2}] \rightarrow [-1, 1]\)
\(x \mapsto \sin x\)
La fonction \(f\) est continue et strictement croissante sur l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}].\)
D'après le théorème dit " des fonctions réciproques " on peut affirmer que
\(f([-\frac{\pi}{2}, \frac{\pi}{2}]) = [f(-\frac{\pi}{2}), f(\frac{\pi}{2})] = [-1, 1]\)
et que \(f\) établit une bijection de\([-\frac{\pi}{2}, \frac{\pi}{2}]\) sur \([-1, 1].\)
La fonction réciproque de \(f\) est appelée Arcsinus et notée \(x \mapsto \arcsin x.\) C'est une bijection de l'intervalle \([-1, 1]\)sur l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}].\)
\(\arcsin : [-1, 1] \rightarrow [-\frac{\pi}{2}, \frac{\pi}{2}]\)
\(x \mapsto \arcsin x\)
Pour tout \(x\) de l'intervalle \([-1, 1],\) \(\arcsin x\)est donc l'unique élément de l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}]\) qui a pour sinus le réel \(x.\)
Remarque :
la notation \(y = \arcsin x\)peut se lire : " y est l'arc (de l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}])\) dont le sinus vaut \(x\)".
Par définition
\(\boxed{\begin{cases} x \in [-1, 1] \\ y = \arcsin x\end{cases} \Leftrightarrow \begin{cases} y \in [-\frac{\pi}{2}, \frac{\pi}{2}] \\ \sin y = x \end{cases}}\)
Exemple :
\(\arcsin \frac{1}{2} = \frac{\pi}{6}\) car \(\frac{\pi}{6} \in [-\frac{\pi}{2}, \frac{\pi}{2}]\) et \(\sin \frac{\pi}{6} = \frac{1}{2}\)
Attention :
\(\forall x \in \mathbb R, \sin x = \frac{1}{2} \Leftrightarrow x = \frac{\pi}{6} + 2k\pi\) ou \(x = 5\frac{\pi}{6} + 2k\pi\) \((k \in \mathbb Z)\)
Il y a une infinité de réels dont le sinus est égal à \(\frac{1}{2}.\) Mais parmi ces réels, seul \(\frac{\pi}{6}\) appartient à l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}].\)
Conséquence de la définition
\(\boxed{\forall x \in [-1, 1]~~~~\sin(\arcsin x) = x}\)
\(\boxed{\forall x \in [-\frac{\pi}{2}, \frac{\pi}{2}]~~~~\arcsin(\sin x) = x}\)
Remarque :
L'expression \(\sin(\arcsin x)\)n'est définie que pour \(x\) appartenant à l'intervalle \([-1, 1].\) Par contre l'expression \(\arcsin(\sin x)\)est définie pour tout réel \(x,\) mais l'égalité \(\arcsin(\sin x)\) n'est vraie que pour \(x\) appartenant à l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}].\)
Par exemple, \(\arcsin(\sin(5\frac{\pi}{6})) = \arcsin(\frac{1}{2}) = \frac{\pi}{6}.\)
Propriété : 1
La fonction Arcsinus est continue et strictement croissante sur \([-1, 1].\)
C'est une conséquence directe du théorème des fonctions réciproques.
\(\begin{array}{|c | c c c|}\hline x & -1 & & 1 \\ \hline & & & \frac{\pi}{2} \\ \arcsin x & & \nearrow & \\ & -\frac{\pi}{2} & & \\ \hline \end{array}\)
Propriété : 2
La fonction Arcsinus est une fonction impaire.
Démonstration :
L'intervalle \([-1, 1]\)est centré en \(0.\)
Soit \(x \in [-1, 1]\) et \(y = \arcsin x\) on a alors \(\sin y = x\) et \(y \in [-\frac{\pi}{2}, \frac{\pi}{2}].\)
La fonction sinus étant impaire, \(\sin(-y) = -x\) et \(-y \in [-\frac{\pi}{2}, \frac{\pi}{2}].\)
D'où \(\arcsin(-x) = -y = -\arcsin x.\)
Graphe
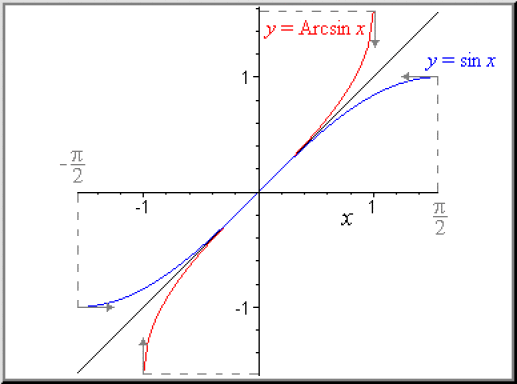
Dans le plan rapporté à un repère orthonormé la courbe représentative de la fonction Arcsinus est la courbe symétrique par rapport à la première bissectrice de la courbe représentative de la restriction de sinus à l'intervalle \([-\frac{\pi}{2}, \frac{\pi}{2}].\)
Dérivée
La fonction \(f\) est dérivable sur \([-\frac{\pi}{2}, \frac{\pi}{2}]\) et \(f'(x) = \cos x.\) La dérivée de \(f\) ne s'annule pas sur \(]-\frac{\pi}{2}, \frac{\pi}{2}[,\) la fonction Arcsinus est donc dérivable sur \(]-1, 1[\)et
\(\forall x \in ]-1, 1[~~~~(\arcsin)'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{\cos(\arcsin x)}.\)
Calcul de \(\cos(\arcsin x)\) : \(\cos^2(\arcsin x) = 1 - \sin^2(\arcsin x) = 1 - x^2\)
et comme \(x \in ]-1, 1[~~~~\arcsin x \in ]-\frac{\pi}{2}, \frac{\pi}{2}[\) et \(\cos(\arcsin x) > 0.\) D'où
\(\boxed{\cos(\arcsin x) = \sqrt{1 - x^2}}\)
On a donc
\(\boxed{\forall x \in ]-1, 1[~~~~(\arcsin)'(x) = \frac{1}{\sqrt{1 - x^2}}}\)
Attention :
La fonction Arcsinus est définie et continue sur l'intervalle fermé \([-1, 1]\)et dérivable sur l'intervalle ouvert \(]-1, 1[.\)