Matrice et applications linéaires

Pour que la question ait un sens, il est nécessaire de se placer dans le cas d'une application linéaire entre deux espaces vectoriels de type fini, de même dimension.

Soit donc deux espaces vectoriels \(E\) et\( \mathcal F\) de dimension \(n\)  et \(\phi\) un isomorphisme de \(E\) dans \(\mathcal F\). La théorie des applications linéaires permet de dire que \(\phi\) est inversible et que son application réciproque est une application linéaire de \(\mathcal F\) dans \(E\). Cela peut se traduire par les égalités :

\(\psi^{-1}\circ\psi=\mathcal Id_E\) et \(\psi\circ\psi^{-1}=\mathcal Id_F\)

qui sont schématisés de la façon suivante :

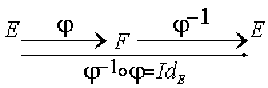
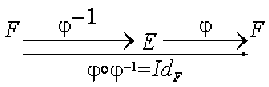
Pour en donner une interprétation matricielle, on choisit des bases\( \mathcal B_E\)  et \(\mathcal B_F\) de\( E\)  et \(\mathcal F\) respectivement. On a alors les schémas suivants :

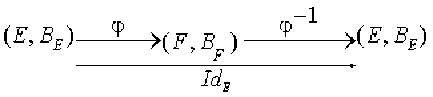
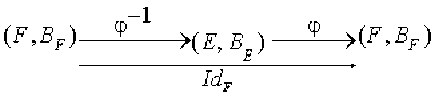
d'où\( [\phi^{-1}\circ\phi]_{\mathcal B_E}=[\mathcal Id_E]_{\mathcal B_E}=\mathcal I_n\) et \([\phi\circ\phi^{-1}]_{\mathcal B_F}=[\mathcal Id_F]_{\mathcal B_F}=\mathcal I_n\)

Compte tenu du théorème général que nous venons d'obtenir pour la matrice associée à la composée d'applications linéaires, cela donne les égalités matricielles suivantes :

\([\phi^{-1}]_{\mathcal B_F}^{\mathcal B_E}[\phi]_{\mathcal B_E}^{\mathcal B_F}=\mathcal I_n\) et \([\phi]_{\mathcal B_E}^{\mathcal B_F}[\phi^{-1}]_{\mathcal B_F}^{\mathcal B_E}=\mathcal I_n\)

Cela prouve que la matrice\( [\phi]_{\mathcal B_E}^{\mathcal B_F}\) est inversible et que son inverse est la matrice \([\phi^{-1}]_{\mathcal B_F}^{\mathcal B_E}\).