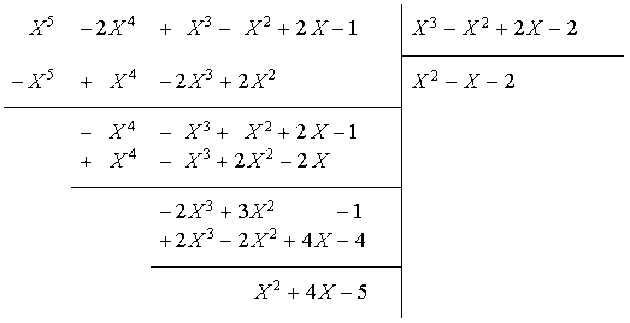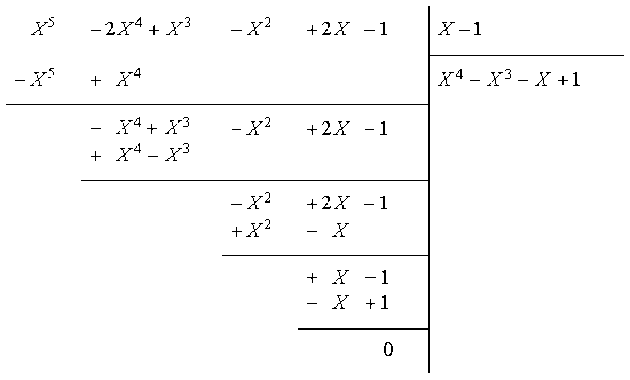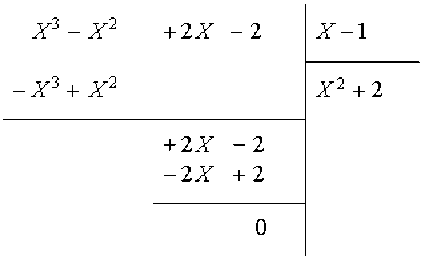PGCD-PPCM de deux polynômes
Partie
Question
Trouver le PGCD dans \(K[X]\) (\(K\) étant \(R\) ou \(C\)) des polynômes \(A\) et \(B\) suivants :
\(A(X)=X^5-2X^4+X^3-X^2+2X-1\)
\(B(X)=X^3-X^2+2X-2\)
Aide simple
Quand on fait la division euclidienne du polynôme A par le polynôme B, on trouve \(A(X)=(X^2-X-2)B(X)+X^2+4X-5\), donc le PGCD des polynômes \(A(X)\) et \(B(X)\) est égal au PGCD des polynômes \(B(X)\) et \(X^2+4X-5\).
On continue par la division de \(B(X)\) par \(X^2+4X-5\), et on recommence le même procédé jusqu'à l'obtention d'un reste nul.
Aide méthodologique
Pour déterminer le PGCD de deux polynômes on applique l'algorithme d'Euclide, utilisant les divisions euclidiennes successives des polynômes et les résultats suivants : dans la division euclidienne de \(F\) par \(G\), si \(F=GQ+R\), alors \(PGCD(F,G)=PGCD(G,R)=PGCD(G,\lambda R)\) où \(\lambda\) est un scalaire non nul.
Solution détaillée
On détermine le PGCD des polynômes \(A\) et \(B\) par le théorème moteur de l'algorithme d'Euclide, utilisant les divisions euclidiennes des polynômes.
On fait la division de \(A\) par \(B\) :
On a obtenu \(A(X)=X^2-X-2)B(X)+X^2+4X-5\).
Donc le PGCD des polynômes \(A(X)\) et \(B(X)\) est égal au PGCD des polynômes \(B(X)\)
et \(X^2+4X-5\).
On fait la division de \(B(X)\) par \(X^2+4X-5\):
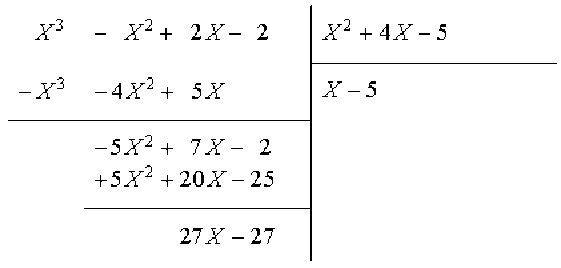
On a obtenu \(B(X)=(X-5)(X^2+4X-5)+27X-27\).
Comme \(27X-27=27(X-1)=27(X-1)\), il est préférable de faire ensuite la division euclidienne
de \(X^2+4X-5\)par \(X-1\), puisque \(PGCD(P,Q)=PGCD(P,\lambda Q)\) si \(\lambda\) est un scalaire non nul.
Le PGCD des polynômes \(B(X)\)et \(X^2+4X-5\) est égal au PGCD des polynômes
\(X^2+4X-5\) et \(X-1\).
On fait la division de \(X^2+4X-5\) par \(X-1\).
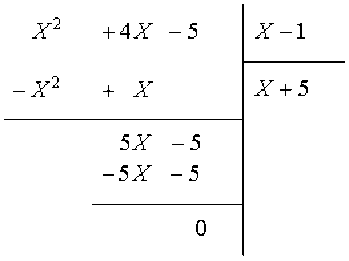
On remarque que le polynôme \(X^2+4X-5\) est un multiple du polynôme \(X-1\).
Donc le polynôme \(X-1\) est le PGCD de \(X^2+4X-5\) et \(X-1\),
donc aussi celui de \(B(X)\) et \(X^2+4X-5\),
donc aussi celui de \(A(X)\) et \(B(X)\).
\(PGCD(A(X),B(X)=X-1\)
Question
Soit \(D\) ce PGCD.
Déterminer \(A'\) et \(B'\) tels que \(A=DA'\) et \(B=DB'\).
Aide méthodologique
Pour déterminer le PGCD de deux polynômes on applique l'algorithme d'Euclide, utilisant les divisions euclidiennes successives des polynômes et les résultats suivants : dans la division euclidienne de \(F\) par \(G\), si \(F=GQ+R\), alors \(PGCD(F,G)=PGCD(G,R)=PGCD(G,\lambda R)\) où \(\lambda\) est un scalaire non nul.
Question
Quel est le PPCM de \(A\) et \(B\).
Aide simple
Se servir de la formule : \(PQ)PGCD(P,Q)\times PPCM(P,Q)\) pour des polynômes \(P\) et \(Q\) unitaires.
Aide méthodologique
Pour déterminer le PGCD de deux polynômes on applique l'algorithme d'Euclide, utilisant les divisions euclidiennes successives des polynômes et les résultats suivants : dans la division euclidienne de \(F\) par \(G\), si \(F=GQ+R\), alors \(PGCD(F,G)=PGCD(G,R)=PGCD(G,\lambda R)\) où \(\lambda\) est un scalaire non nul.
Solution détaillée
Pour calculer le PPCM de A et B, on se sert de la formule (les polynômes A et B étant unitaires) : \(AB=PGCD(A,B)\times PPCM(A,B)\).
On peut calculer explicitement le produit \(AB\), puis diviser le résultat par le PGCD de A et B, mais il est préférable de se servir de la question 2. :
\(A=DA'\) et \(B=DB'\) où \(A'(X)=X^4-X^3-X+1\) et \(B'(X)=X^2+2\).
Comme \(AB=DA'DB'=D\times PPCM(A,B)\), on en déduit que \(PPCM(A,B)=DA'B'\), c'est à dire :
\(\begin{array}{ccc}PPCM(A(X),B(X))&=&(X-1)(X^4-X^3-X+1)(X^2+2)\\&=&X^7-2X^6+3X^5-5X^4+4X^3-3X^2+4X-2\end{array}\)
On pouvait remarquer que : \(PPCM(A,B) = AB' = A'B\), puisque \(A = DA'\) et \(B = DB'\), et l'on pouvait alors calculer un de ces deux produits.