Arithmétique dans K[X]

1. On détermine le PGCD des polynômes A et B par l'algorithme d'Euclide, utilisant les divisions euclidiennes des polynômes.

Ce PGCD est le dernier reste non nul à une constante multiplicative près, car le PGCD est un polynôme unitaire (si le reste est unitaire, c'est le PGCD, sinon on divise le dernier reste non nul par le coefficient du terme dominant pour obtenir le PGCD).

\(A(X)=X^3+6X^2+11X+6\)

\(B(X)=X^3+4X^2+X-6\)

Comme les polynômes A et B ont le même degré, on a immédiatement :

\(A(X)=B(X)+2X^2+10X+12\)

On divise \(B(X)\) par \(2X^2+10X+12\):

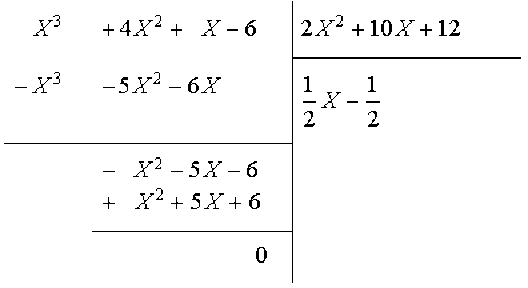
Donc le dernier reste non nul est le polynôme \(2X^2+10X+12\). Ce polynôme n'étant pas unitaire, on le divise par le coefficient du terme dominant.

\(PGCD(A(X),B(X))=X^2+5X+6\)

2. On détermine de même le PGCD de A et C

\(A(X)=X^3+6X^2+11X+6\)

\(C(X)=X^3+X^2-X-1\)

Comme les polynômes A et C ont le même degré, on a immédiatement :

\(A(X)=C(X)+5X^2+12X+7\)

Donc on divise \(C(X)\) par \(5X+12X+7\):

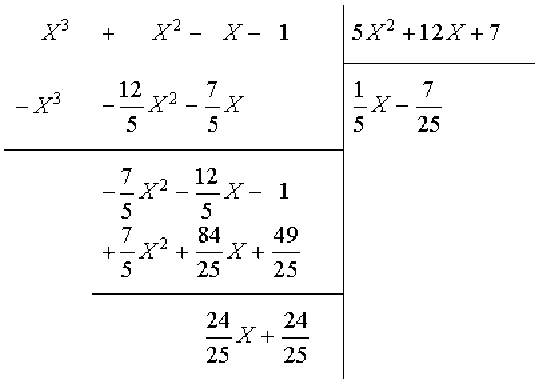
Au lieu de continuer les divisions pour trouver le dernier reste non nul, vu la forme du diviseur suivant qui est le polynôme \(\frac{24}{25}X+\frac{24}{25}\), il vaut mieux utiliser le fait que le PGCD des polynômes \(A(X)\) et \(C(X)\) est égal au PGCD des polynômes \(C(X)\) et \(5X^2+12X+7\) et que le PGCD des polynômes \(C(X)\) et \(5X^2+12X+7\) est égal au PGCD des polynômes

\(5X^2+12X+7\) et \(\frac{24}{25}X+\frac{24}{25}\).

Or \(\frac{24}{25}X+\frac{24}{25}=\frac{24}{25}(X+1)\)

Donc le PGCD des polynômes \(C(X)\) et \(5X^2+12X+7\) est égal au PGCD des polynômes \(5X^2+12X+7\) et \(X+1\).

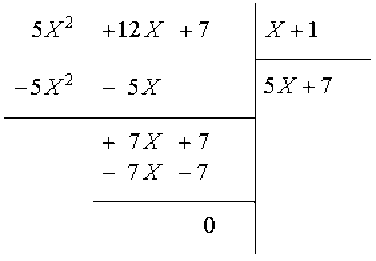
Comme le polynôme \(X+1\) divise \(5X^2+12X+7\), il est le PGCD des polynômes

\(5X^2+12X+7\) et \(X+1\), donc celui de \(C(X)\) et \(5X^2+12X+7\),

donc celui de \(A(X)\) et \(C(X)\).

\(PGCD(A(X),C(X))=X+1\)

3. On détermine le PGCD de B et C.

\(B(X)=X^3+4X^2+X-6\)

\(C(X)=X^3+X^2-X-1\)

Comme les polynômes B et C ont le même degré, on a immédiatement :

\(B(X)=C(X)+3X^2+2X-5\)

On divise \(C(X)\) par \(3X^2+2X-5\).

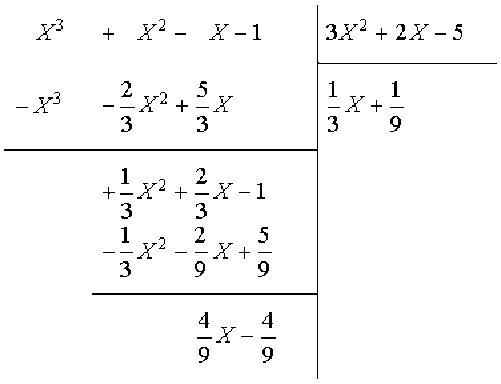
Ici aussi, vu la forme du reste, il vaut mieux utiliser la méthode qui consiste à dire que le PGCD des polynômes \(B(X)\) et \(C(X)\) est égal au PGCD des polynômes \(C(X)\).

et \(3X^2+2X-5\), qui lui est égal au PGCD des polynômes \(3X^2+2X-5\) et \(\frac{4}{9}X-\frac{4}{9}\).

Or \(\frac{4}{9}X-\frac{4}{9}=\frac{4}{9}(X-1)\)

Donc le PGCD des polynômes \(3X^2+2X-5\) et \(\frac{4}{9}X-\frac{4}{9}\) est égal au PGCD des polynômes \(3X^2+2X-5\) et \(X-1\).

On divise \(3X^2+2X-5\) par \(X-1\):

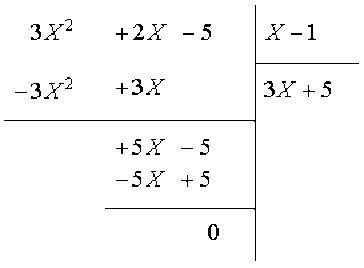
Le PGCD des polynômes \(3X^2+2X-5\) et \(X-1\) est donc \(X-1\), et comme précédemment on en déduit que :

\(PGCD(B(X),C(X))=X-1\)

4. Il reste à calculer le PGCD de \(A\), \(B\) et \(C\).

L'algorithme d'Euclide ne concerne que la recherche du PGCD de deux polynômes, donc on utilise ici la définition du PGCD de plusieurs polynômes.

Par définition, le PGCD, noté D, des polynômes \(P_1,P_2,\ldots,P_n\) non tous nuls est le seul polynôme unitaire satisfaisant aux conditions a. et b. suivantes :

a. Le polynôme \(D\) divise tous les polynômes \(P_i\),

b. Tout polynôme divisant chacun des \(P_i\) divise \(D\).

On déduit de la condition a. que le PGCD de \(A\), \(B\) et \(C\) divise \(A\) et \(C\).

Ceci entraîne d'après la condition b. que le PGCD de \(A\), \(B\) et \(C\) divise le PGCD de \(A\) et \(C\).

De même le PGCD de \(A\), \(B\) et \(C\) divise \(B\) et \(C\) donc il divise le PGCD de \(B\) et \(C\).

Or \(PGCD(A(X),C(X))=X+1\) et \(PGCD(B(X),C(X))=X-1\).

Donc le PGCD de \(A(X)\), \(B(X)\) et \(C(X)\) divise les deux polynômes \(X+1\) et \(X-1\).

Il est immédiat que les polynômes \(X+1\) et \(X-1\) sont premiers entre eux

(par exemple ces deux polynômes vérifient l'identité de Bézout \(\frac12(X+1)-\frac12(X-1)=1\)). D'où

\(PGCD(A(X),B(X),C(X))=1\)

Remarque :

Les polynômes \(A\), \(B\) et \(C\) ne sont pas premiers deux à deux, mais ils n'ont pas de diviseur commun : ils sont premiers dans leur ensemble.