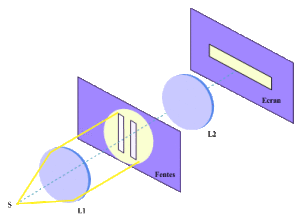
Diffraction par deux fentes fines identiques et parallèles sous incidence normale
Le plan des deux fentes fines est éclairé par une onde plane monochromatique obtenue par exemple en plaçant une source ponctuelle monochromatique au foyer principal objet d'une lentille ; cette onde arrive sous incidence normale, donc tous les points du plan des deux fentes sont en phase puisqu'ils ont le même déphasage par rapport à la source ponctuelle.
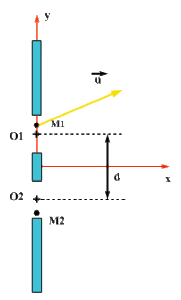
Considérons l'onde diffractée dans une direction caractérisée par un vecteur unitaire \(\vec u\).
Soit \(M_1\) un point de la fente 1 et considérons la vibration émise par \(M_1\) dans la direction \(\vec u\). Soit \(O_1\) le centre de la fente 1 pris pour origine.
La différence de marche s'écrit :
\(\delta (M_1) = \overrightarrow{O_1M_1} ~.~ \vec u = x_1 . \cos \theta_x + y_1 . \cos \theta_y = \alpha . x_1 + \beta . y_1\)
Soit \(d\) la distance entre \(O_1\) et \(O_2\). La vibration diffractée dans la direction \(\vec u\) issue de \(O_2\) est déphasée par rapport à celle émise en \(O_1\) de :
\(\Phi_{O_1O_2} = \frac{2 \pi}{\lambda} ~ \delta_{O_1O_2}\)
et \(\delta_{O_1O_2} = \overrightarrow{O_1O_2} ~.~ \vec u = d . \alpha\)
De même pour une vibration émise par \(M_2\), elle présente une différence de marche par rapport à celle émise par \(O_1\) dans la direction \(\vec u\) qui s'écrit :
\(\delta_{O_1M_2} = \overrightarrow{O_1M_2} ~.~ \vec u = \overrightarrow{O_1O_2} ~.~ \vec u ~+~ \overrightarrow{O_2M_2} ~.~ \vec u = \alpha . d + \alpha . x_2 + \beta . y_2\)
La vibration résultante arrivant en \(P\), point à l'infini dans la direction \(\vec u\) s'obtient en tenant compte de toutes les vibrations émises par les deux fentes identiques et parallèles :
\(\begin{array}{lll}A_{(P)} & = & \displaystyle{\iint_{f_1} \mathrm d A_{(M_1)} + \iint_{f_2} \mathrm d A_{(M_2)}}\\& = & \displaystyle{A_0 \int_{-\frac{b}{2}}^{\frac{b}{2}} \int_{-\frac{a}{2}}^{\frac{a}{2}} \mathrm e^{i \frac{2 \pi}{\lambda} (\alpha x_1 + \beta y_1)} \mathrm d x_1 \mathrm d y_1 + A_0 \int_{-\frac{b}{2}}^{\frac{b}{2}} \int_{-\frac{a}{2}}^{\frac{a}{2}} \mathrm e^{i \frac{2 \pi}{\lambda} (\alpha x_2 + \beta y_2 + d \alpha)} \mathrm d x_2 \mathrm d y_2 }\\& = & \displaystyle{\Big[ A_0 \iint \mathrm e^{i \frac{2 \pi}{\lambda} (\alpha x + \beta y)} \mathrm d x \mathrm d y \Big] \Big( 1 + \mathrm e^{i \frac{2 \pi}{\lambda} d \alpha}\Big)}\end{array}\)
L'intensité en \(P\) s 'écrit :
\(\begin{array}{lll} I_{(P)} & = & A_{(P)} . A_{(P)}^{\ast} \\ & = & I_0 . a^2 . b^2 \frac{\sin^2\frac{\Phi}{2}}{\Big(\frac{\Phi}{2}\Big)^2} \frac{\sin^2\frac{\Phi'}{2}}{\Big(\frac{\Phi'}{2}\Big)^2} \Big(1 + e^{i 2 \pi \frac{d \alpha}{\lambda}}\Big) \Big(1 + e^{- i 2 \pi \frac{d \alpha}{\lambda}}\Big) \end{array}\)
On reconnaît dans le premier terme l'intensité diffractée par une fente rectangulaire : \(I_{diff}\)
Le second terme s'écrit :
\(\begin{array}{lll} \Big(1 + e^{i 2 \pi \frac{d \alpha}{\lambda}}\Big) \Big(1 + e^{- i 2 \pi \frac{d \alpha}{\lambda}}\Big) & = & 1 + 1 + e^{i 2 \pi \frac{d \alpha}{\lambda}} + e^{- i 2 \pi \frac{d \alpha}{\lambda}} \\ & = & 2 + 2 \cos \Big( 2 \pi \frac{d \alpha}{\lambda} \Big) \\ & = & 2 \Big( 1 + \cos \Big( 2 \pi \frac{d \alpha}{\lambda} \Big) \Big)\end{array}\)
On reconnaît le terme d'interférences donné par deux sources cohérentes entre elles \(O_1\) et \(O_2\).
Si la fente est très fine \(a \ll b\) l'intensité résultante en \(P\) s'écrit :
\(I_{(P)} = 2 ~ I_0 \frac{\sin^2 \frac{\Phi}{2}}{\Big(\frac{\Phi}{2}\Big)^2} \Big(1 + \cos \Big(2 \pi \frac{\alpha d}{\lambda} \Big) \Big)\)
avec \(\Phi = 2 \pi \frac{\alpha a}{\lambda}\)