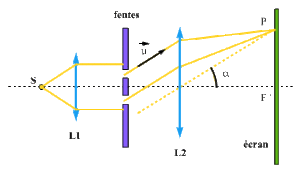
Figure de diffraction
Elle s'observe dans le plan focal image d'une lentille convergente placée après le plan des fentes
A la direction \(\alpha\) correspond le point \(P\) tel que :
\(x_P = \alpha f\)
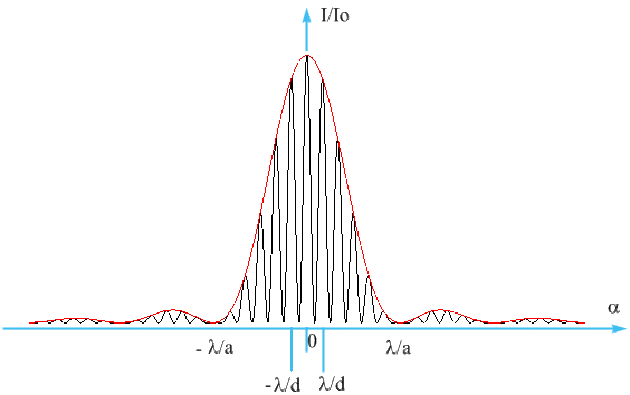
Dans la tache principale de diffraction de largeur \(\Delta x = f' \frac{\lambda}{a}\) on observe des franges d'interférences brillantes et sombres. Les franges brillantes correspondent à :
\(I_{max}\) si \(\cos \Big(\frac{2 \pi}{\lambda} \alpha d \Big) = + 1\)
\(\frac{2 \pi}{\lambda} \alpha d = 2 k \pi\) \(~~ \Rightarrow \alpha = k \frac{\lambda}{d}\)
Les franges d'intensité maximale sont donc repérées par :
\(x_{max} = f' . k . ~ \frac{\lambda}{d}\)
Les franges d'intensité nulle s'obtiennent quand on a :
\(I_{min}\) si \(\cos \Big( \frac{2 \pi}{\lambda} \alpha d \Big) = - 1\)
\(\frac{2 \pi}{\lambda} \alpha d = (2 k + 1) \pi\) \(~~ \Rightarrow \alpha = \frac{(2 k + 1)}{2} \frac{\lambda}{d}\)
\(x_{min} = f' \frac{(2 k + 1)}{2} \frac{\lambda}{d}\)
L'intensité des franges d'interférences est donc modulée par le profil de diffraction.

Les franges d'interférences s'observent principalement dans la tache centrale de diffraction. C'est la figure observée dans le dispositif des fentes d'Young.
La diffraction obtenue à partir de 2 fentes fines est visualisée dans l'animation suivante :