Enoncé
Le théorème de Gauss s'énonce de la façon suivante :
Théorème :
Le flux du champ électrique envoyé à travers une surface fermée \(S_g\) quelconque vaut \(1 / \epsilon_0\) fois la charge algébrique totale, contenue dans le volume délimité par cette surface.
\(\Phi=\oiint_{S_g}\vec{E}d\vec{S}=\frac{Q_{\textrm{int\'erieure \`a }S_g}}{\epsilon_0}\)
Démonstration :
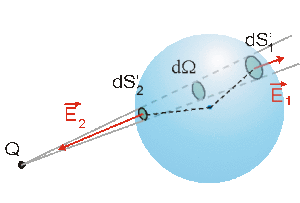
a) cas de charges extérieures à une surface \(S_g\) fermée
Les éléments \(\mathrm d S'_1\) et \(\mathrm d S'_2\) sont vus sous le même angle \(\mathrm d \Omega\) en valeur absolue. Cependant, \(\vec E_1\) et \(\mathrm d \vec S'_1\) sont colinéaires alors que \(\vec E_2\) et \(\mathrm d \vec S'_2\) sont opposés. Les flux \(\mathrm d \Phi = \vec E_1 . \mathrm d \vec S'_1\) et \(\mathrm d \Phi' = \vec E' . \mathrm d \vec S'\) sont donc de signe opposé. Les flux élémentaires s'annulant 2 à 2, le flux total du champ \(\vec E\) créé par la charge \(Q\) extérieure à la surface fermée est nul.
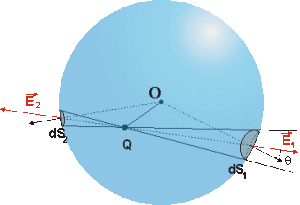
b) cas de charges intérieures à une surface \(S_g\) fermée.
La somme des flux élémentaires ne sera pas nulle car tous les vecteurs élément de surface sont par exemple tous orientés de la surface vers l'extérieur. Le flux total envoyé par \(Q\) à travers \(S\) sera la somme des flux élémentaires soit :
\(\displaystyle{\Phi = \frac{Q}{4 \pi \epsilon_0} \int \mathrm d \Omega}\)
L'unité d'angle solide est l'angle qui découpe sur une sphère de rayon unité une surface unité. Comme la surface de la sphère de rayon unité est \(4 \pi R² = 4 \pi\), l'angle solide qui d'un point voit tout l'espace a pour valeur \(4 \pi\). La somme étant étendue à tout l'espace soit \(\Phi = \frac{Q}{\epsilon_0}~\) ,
si il se trouve, à l'intérieur de \(S\) , \(n\) charges \(Q_1, Q_2 , Q_3 , ..., Q_n\) :
\(\displaystyle{\Phi = \frac{1}{\epsilon_0} \sum_{i=1}^n Q_i}\)
En posant : \(~\Phi = \frac{Q_i}{\epsilon_0}\)
Le flux de \(E\) envoyé à travers une surface fermée est égal au quotient par \(\epsilon_0\) de la somme des charges intérieures, quelles que soient les charges extérieures.
L'application du théorème de Gauss est très utile dans des problèmes qui présentent un haut degré de symétrie. Vérifiez cette propriété sur l'exemple très simple du champ \(\vec E\) créé par une source ponctuelle \(Q\) .
Les deux simulations qui suivent vont vous permettre d'appliquer le théorème de Gauss dans le cas de deux structures uniformément chargées et présentant des axes de symétrie .Vous pouvez mettre en évidence la simplicité avec laquelle le théorème de Gauss permet de calculer le champ électrostatique créé par ces deux distributions de charges qui présentent un haut degré de symétrie.