Le vecteur, gradient de potentiel
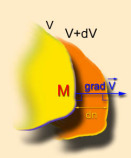
Soient deux surfaces équipotentielles \(V\) et \(V + \mathrm d V\). Le potentiel étant une fonction continue, à un déplacement infiniment petit \(\mathrm d n\) correspond une variation infiniment petite du potentiel \(\mathrm d V\). Il s'ensuit que les surfaces \(V\) et \(V + \mathrm d V\) sont très rapprochées et d'autant plus que \(\mathrm d V\) est petit.
Soit un point \(M\), quelconque de la surface équipotentielle \(V\). On définit, en ce point, un vecteur appelé gradient de potentiel désigné par \(\overrightarrow{\mathrm{grad}}~V\), de la façon suivante :
Son origine est le point \(M\).
Il est porté par la normale à la surface équipotentielle passant par le point \(M\).
Il est orienté dans le sens des valeurs croissantes du potentiel.
Pour calculer son module, considérons un déplacement infiniment petit sur la normale à partir du point \(M\). Soit \(\mathrm d n\) la longueur de ce déplacement et \(\mathrm d V\) l'augmentation correspondante du potentiel. Par définition,
\(\big|\big| \overrightarrow{\mathrm{grad}}~V \big|\big| = \left| \begin{array}{lc} \frac{\mathrm d V}{\mathrm d n} \end{array} \right |\)
Ce rapport caractérise la variation de potentiel au point \(M\) suivant la direction normale. Il s'exprime évidemment en volt par mètre ( \(V/m\) ). C'est l'unité internationale de gradient de potentiel.
Par analogie on peut écrire :
\(\vec E = - \overrightarrow{\mathrm{grad}}~V\)