Aspect mathématique [Le champ magnétostatique]

Aspect mathématique

Transformation d'un vecteur vrai^[1] par une symétrie par rapport à un plan\((\pi)\)

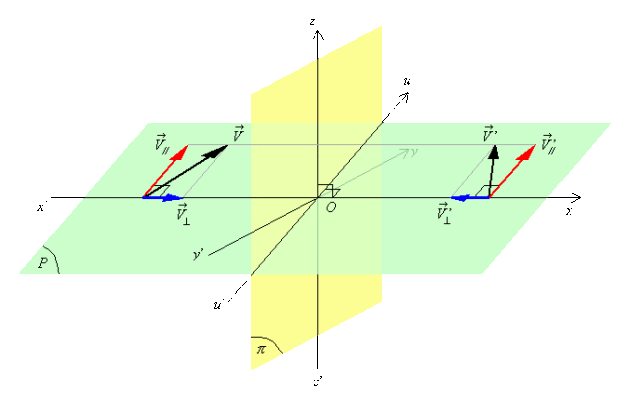
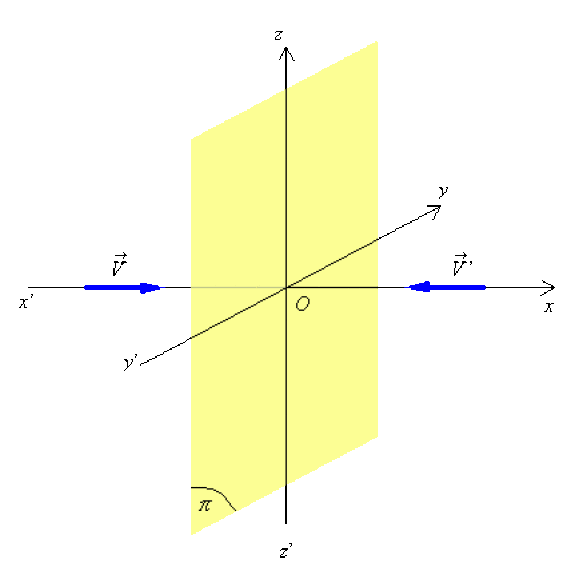
Soit un vecteur \(\vec V\) et un plan quelconque \((\pi)\) ; les figures ci-dessous montrent comment ce vecteur se transforme en un vecteur \(\vec V^,\) par symétrie par rapport à \((\pi)\) .

\(\vec V\) est perpendiculaire à \((\pi)\) alors \(\vec V^, = -\vec V\)

Complément : Visualisations des espaces 3D

Les représentations \(3\mathrm{D}\) sont visualisées par un applet Java.

\(\vec V\) est parallèle à \((\pi)\) alors \(\vec V^, = \vec V\).

Complément : Visualisations des espaces 3D

Les représentations \(3\mathrm{D}\) sont visualisées par un applet Java.

\(\vec V\) est quelconque par rapport à \((\pi)\) alors :
- pour les composantes perpendiculaires à \((\pi)\) on a : \(\vec V^,_\perp = -\vec V_\perp\)
- pour les composantes parallèles à \((\pi)\) on a : \(\vec V^,_{ //} = \vec V_{ //}\)

Complément : Visualisations des espaces 3D

Les représentations \(3\mathrm{D}\) sont visualisées par un applet Java.

Les composantes parallèles à \((\pi)\) se conservent.

Transformation d'un pseudo-vecteur^[2] par une symétrie par rapport à un plan \((\pi)\) .

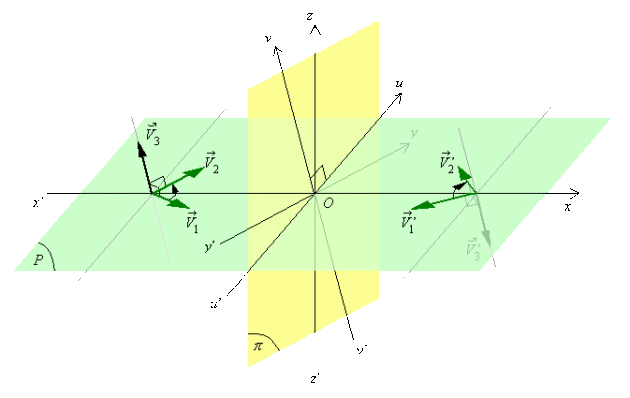
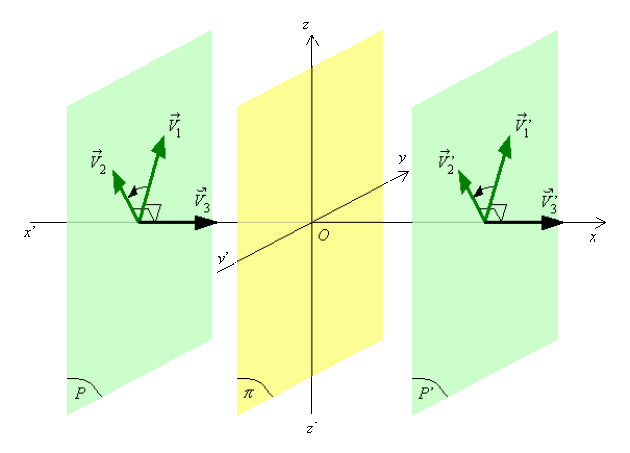
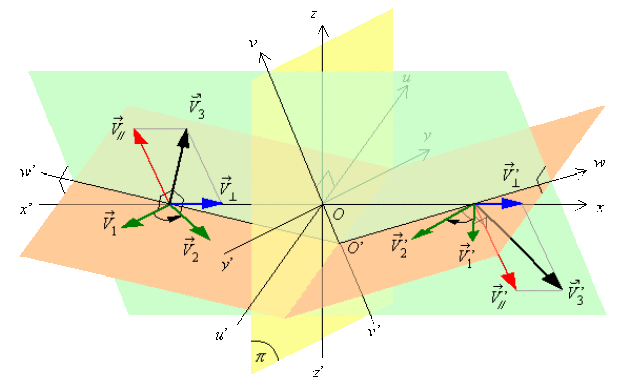
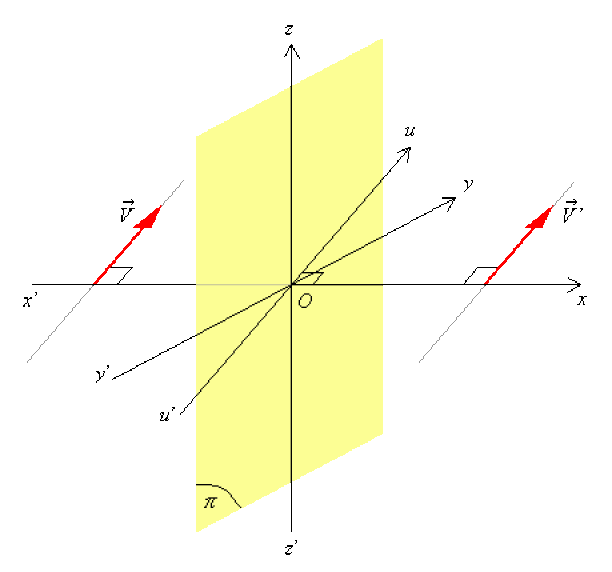
Soit un pseudo-vecteur \(\stackrel{\hookrightarrow}{V}_{3}\) défini par le produit vectoriel^[3] \(\stackrel{\hookrightarrow}{V}_{3} = \vec V_1 \wedge \vec V_2\) et un plan quelconque \((\pi)\) ; les figures ci-dessous montrent comment ce pseudo-vecteur se transforme en un pseudo-vecteur \(\stackrel{\hookrightarrow}{V'}_{3}\) par symétrie par rapport à \((\pi)\)

\(\vec V_1\) et \(\vec V_2\) sont dans un plan \((P)\) perpendiculaire au plan \((\pi)\), alors\( \vec V^,_1\) et \(\vec V^,_2\) sont dans le même plan \((P)\) :\( \stackrel{\hookrightarrow}{V'}_{3}\)et \(\stackrel{\hookrightarrow}{V}_3\) sont parallèles au plan \((\pi)\) et \(\stackrel{\hookrightarrow}{V'}_{3}= -\stackrel{\hookrightarrow}{V}_{3}\) .

Complément : Visualisations des espaces 3D

Les représentations \(3\mathrm{D}\) sont visualisées par un applet Java.

\(\vec V_1\) et \(\vec V_2\) sont contenus dans un plan parallèle à \((\pi)\), alors \(\vec V^,_1\) et \(\vec V^,_2\) sont également compris dans un plan parallèle à \((\pi)\) : \(\stackrel{\hookrightarrow}{V'}_{3}\) et \(\stackrel{\hookrightarrow}{V}_3\) sont perpendiculaires à \((\pi)\) et \(\vec V^,_3"retation = \vec V_3"retation\).

Complément : Visualisations des espaces 3D

Les représentations \(3\mathrm{D}\) sont visualisées par un applet Java.

\(\vec V_1\) et \(\vec V_2\) sont quelconques par rapport à \((\pi)\) , alors \(\stackrel{\hookrightarrow}{V'}_{3 \perp} = \stackrel{\hookrightarrow}{V}_{3 \perp}\) et \(\stackrel{\hookrightarrow}{V'}_{3 //} = \stackrel{\hookrightarrow}{V}_{3 //}\)

Complément : Visualisations des espaces 3D

Les représentations \(3\mathrm{D}\) sont visualisées par un applet Java.

Les composantes perpendiculaires à \((\pi)\) se conservent.

Notes

Vecteur vrai
Un vecteur vrai ou vecteur polaire est défini par :
- une direction,
- un sens sur cette direction,
- sa norme.
Exemples de vecteurs vrais : la vitesse \(\vec v\), la force \(\vec F\), le champ électrostatique \(\vec E\), le potentiel vecteur \(\vec A\) .
Pseudo-vecteur
On dit aussi vecteur axial. Il est défini par :
- une direction qui est généralement un axe de rotation,
- un sens sur cet axe, lié à la convention adoptée pour l'orientation de l'espace,
- sa norme.
On le distingue des vecteurs polaires par une flèche courbe : \(\stackrel{\hookrightarrow}{B}\)
Produit vectoriel (définition géométrique)
- Dans une base orthonormée directe \(\mathfrak{B} = (\vec e_1, \vec e_2, \vec e_3)\), le produit vectoriel de deux vecteurs \(\vec V_1\) et \(\vec V_2\) faisant entre eux un angle \(\theta \in [0, \pi]\) est un vecteur \(\stackrel{\hookrightarrow}{p}\) noté \(\stackrel{\hookrightarrow}{P}= \vec V_1 \wedge \vec V_2\),
  sa direction est perpendiculaire au plan défini par \(\vec V_1\) et \(\vec V_2\),
  son sens est tel que le trièdre \(\vec V_1\), \(\vec V_2\), \(\stackrel{\hookrightarrow}{P}\) soit direct (règle du tire bouchon de Maxwell),
  sa norme \(\mathrm{||} P \mathrm{||}\) est telle que \(\mathrm{||} P \mathrm{||} = \mathrm{||}\vec V_1\mathrm{||}~~\mathrm{||}\vec V_2\mathrm{||}~\sin \theta\).
\(\mathrm{||}\vec V_1 \wedge \vec V_2\mathrm{||}\) représente l'aire du parallélogramme construit sur les vecteurs \(\vec V_1\) et \(\vec V_2\)
En effet : \(\mathrm{||}\vec V_1 \wedge \vec V_2\mathrm{||} = \mathrm{||}\vec V_1\mathrm{||}. (\mathrm{||}\vec V_2\mathrm{||} ~\sin ~ \theta) = \mathrm{||}\vec V_1\mathrm{||} . h\)
- Détermination de \(\stackrel{\hookrightarrow}{P}\)
  Considérons le produit vectoriel \(\stackrel{\hookrightarrow}{P}= \vec V \wedge \vec V'\).
  Dans \(\mathfrak{B}\), les composantes de \(\stackrel{\hookrightarrow}{P}\)s'expriment en fonction de celles de \(\vec V\) et \(\vec V'\) en utilisant la disposition pratique suivante :