Théorème d'Ampère appliqué à un solénoïde (1)
Partie
Question
Soit un solénoïde parcouru par un courant d'intensité \(I\), constitué de \(n\) spires par unité de longueur.
Exprimer la circulation du champ magnétostatique \(\vec B\) le long du contour fermé et orienté \(\mathcal{C}\) situé à l'intérieur du solénoïde.
Aide simple
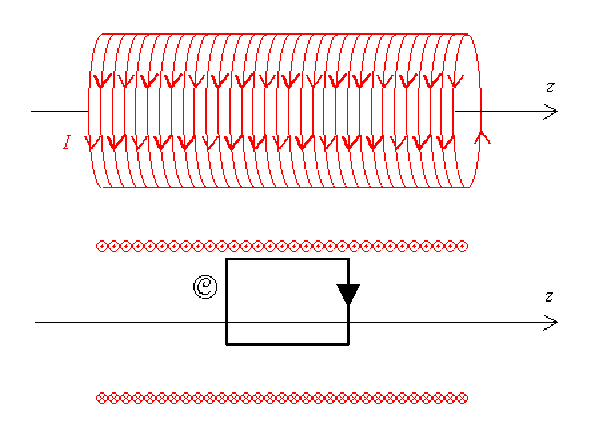
La circulation de \(\vec B\) le long d'un contour fermé \(\mathcal{C}\) est donnée par le théorème d'Ampère.
Rappel de cours
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
D'après le théorème d'Ampère, la circulation de \(\vec B\) le long d'un contour fermé \(\mathcal{C}\) s'écrit :
\(\displaystyle{ \oint_{\mathcal{C}} \vec B . \vec{\mathrm{d}l} = \mu_0 . \sum I }\)
où le terme \(\displaystyle{ \sum I}\) fait la somme algébrique des courants qui traversent \(\mathcal{C}\).
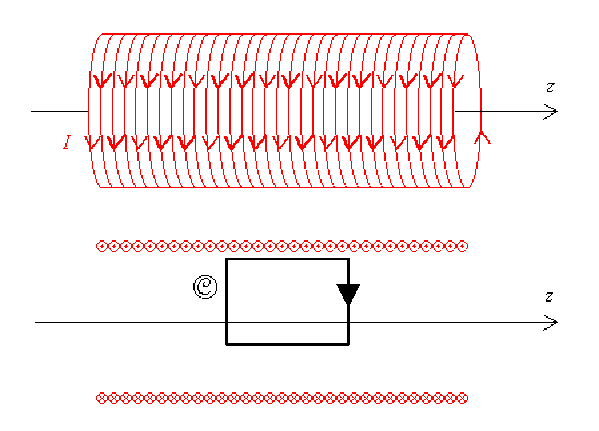
Ici aucun courant ne traverse \(\mathcal{C}\).
En effet, ce contour étant à l'intérieur du solénoïde, les spires du solénoïde l'encerclent, mais ne le traversent pas.
En conclusion : \(\displaystyle{ \oint_{\mathcal{C}} \vec B . \vec{\mathrm{d}l} = 0}\)