Flux du champ magnétostatique créé par un courant filiforme, rectiligne et infiniment long à travers une surface fermée [Les propriétés du champ magnétostatique]

Flux du champ magnétostatique créé par un courant filiforme, rectiligne et infiniment long à travers une surface fermée

Considérons la distribution de courant \(\mathfrak{(D)}\) constituée par un conducteur rectiligne, filiforme, supposé infiniment long^[1] et parcouru par un courant continu, d'intensité \(\mathsf{I}\).

Ce fil est confondu avec l'axe \(Oz\) d'un repère orthonormé direct \(\mathcal{R} = (O ; x,y,z)\) et \(\mathsf{I}\) circule dans le sens des \(z\) positifs.

Ce que nous savons déjà
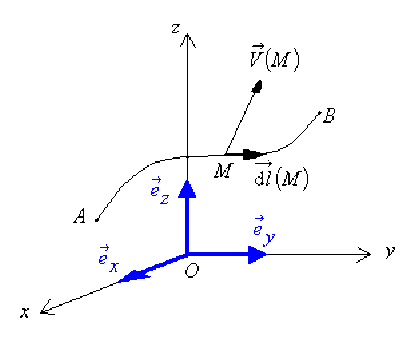
- Le champ magnétostatique \(\stackrel{\hookrightarrow}{B}(M)\) créé en tout point \(\mathsf{M}\) de l'espace par cette distribution de courant \(\mathfrak{(D)}\) est orthoradial et a pour expression \(\vec B(M) = \frac {\mu_0I}{2\pi\rho} \vec e_{\phi}\).
- Les lignes de champ sont fermées. Ici, ce sont des cercles d'axe \(Oz\) en tout point desquels \(\stackrel{\hookrightarrow}{B}(M)\) est tangent et sur lesquels \(\mathsf{B}\) garde la même valeur ; ce n'est pas le cas général.

Soit à calculer le flux^[2] de \(\stackrel{\hookrightarrow}{B}(M)\) à travers une surface fermée^[3] \(\circledS\) constituée par un cylindre fermé d'axe \(Oz\).
- Les surfaces de base \(\mathfrak{(S}_1)\) et \(\mathfrak{(S}_2)\) de rayon \(\rho\) de ce cylindre sont constituées par la juxtaposition d'une infinité de lignes de champ dont les rayons sont compris entre \(0\) et \(\rho\); la surface latérale \(\mathfrak{(S}_{\mathrm{lat}})\) est constituée par la juxtaposition d'une infinité de lignes de champ de rayon \(\rho\).

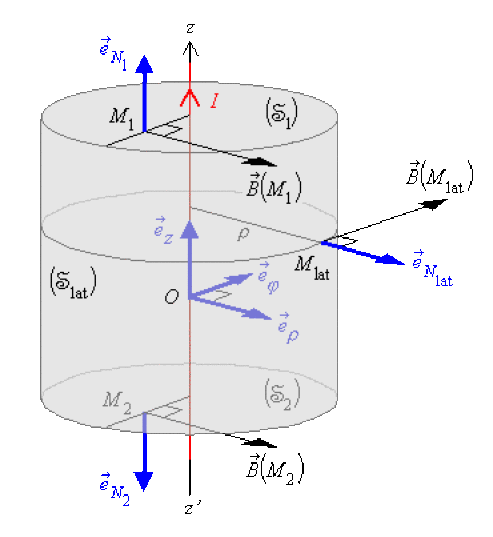
Puisque \(\vec B(M) = \frac{\mu_0 I}{2\pi\rho}\vec e_{\phi}\) , si le point \(\mathsf{M}\) appartient soit à \(\mathfrak{(S}_1)\), \(\mathfrak{(S}_2)\) ou \(\mathfrak{(S}_{\mathrm{lat}})\) , le champ \(\stackrel{\hookrightarrow}{B}(M)\) est tangent à toutes ces surfaces et il est orthogonal aux vecteurs unitaires \(\vec e_{N_1}\), \(\vec e_{N_2}\) et \(\vec e_{N_{\mathrm{lat}}}\) des normales à ces surfaces, avec \(\vec e_{N_1} = \vec e_z\), \(\vec e_{N_2} = -\vec e_z\) et \(\vec e_{N_{\mathrm{lat}}} = \vec e_{\rho}\).
On a donc :
\(\Phi_{\vec B} = \oiint_{\mathfrak{S}} \vec B~.~\overrightarrow{\mathrm{d}\mathfrak{S}} = \iint_{\mathfrak{S}_1}\vec B(M_1) . \mathrm{ }\overrightarrow{\mathrm{d}\mathfrak{S}_1} + \iint_{\mathfrak{S}_2}\vec B(M_2) . \mathrm{ }\overrightarrow{\mathrm{d}\mathfrak{S}_2} + \iint_{\mathfrak{S}_{\mathrm{lat}}}\vec B(M_{\mathrm{lat}}) . \mathrm{ }\overrightarrow{\mathrm{d}\mathfrak{S}_{\mathrm{lat}}} = 0\)
Le flux de \(\stackrel{\hookrightarrow}{B}(M)\) à travers la surface fermée du cylindre est nul.

Notes

Infinie (distribution), infiniment long
Deux attitudes sont possibles lorsqu'il s'agit d'étudier les propriétés de l'espace dues à des distributions telles qu'un fil, un cylindre, un disque,... :
- on imagine que la distribution est infinie (une droite, un cylindre infini, un plan,...) et on peut considérer n'importe quel point \(\mathsf{M}\) de l'espace ;
- on sait que la distribution ayant forcément des dimensions finies, le domaine d'étude est restreint à une région limitée, voire très limitée, centrée sur la distribution.
Flux d'un champ vectoriel à travers une surface
On appelle flux du champ vectoriel \(\vec V(M)\) à travers une surface, le scalaire \(\Phi\) défini par l'intégrale de surface :
- \(\Phi = \iint_{\mathfrak{S}}\vec V(M) . rotation" {\mathrm{d}\mathfrak{S}}(M)\) lorsque \(\mathsf{M}\) est un point d'une surface ouverte \(\mathfrak{(S)}\).
- \(\Phi = \oiint_{\mathfrak{S}}\vec V(M) . rotation" {\mathrm{d}\mathfrak{S}}(M)\) lorsque \(\mathsf{M}\) est un point d'une surface fermée \(\circledS\).
  Dans ce cas, le champ vectoriel \(\vec V(M)\) est à flux conservatif si le flux de \(\vec V(M)\) à travers une surface fermée quelconque \(\circledS\) est nul.
Surface fermée
Une surface fermée \(\circledS\) est une surface dépourvue de toute "ouverture". On peut se représenter ce type de surface en l'imaginant matérielle et rigide ; elle pourrait contenir un liquide sans qu'il puisse s'en échapper. On oriente une surface fermée \(\circledS\) en définissant en tout point \(M\) de \(\circledS\), un vecteur unitaire \(\vec e_N\) orthogonal à \(\circledS\) : par convention, il est toujours orienté vers l'extérieur de la surface \(\circledS\).