Le pendule simple
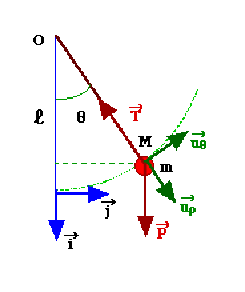
Le pendule simple consiste en une masse ponctuelle \(m\) à l'extrémité d'une tige sans masse de longueur pouvant pivoter librement autour de son extrémité supérieure. La question est de déterminer la fréquence propre d'oscillation de ce pendule.
On peut établir l'équation différentielle du mouvement de trois façons différentes:
par l'application du Principe Fondamental de la Dynamique, on trouve:
\(\displaystyle{\overrightarrow T+\overrightarrow P=m\overrightarrow\gamma}\)
par la conservation de l'énergie en exprimant :
\(\displaystyle{U(\theta)-U(0)=mgl(1-\cos\theta)}\)
\(\displaystyle{T(\theta)=\frac{1}{2}\textrm{mv}^2=\frac{1}{2}\textrm ml^2\dot\theta^2}\)
et en dérivant l'énergie totale par rapport au temps on trouve la même équation :
\(\displaystyle{\ddot\theta+\frac{g}{l}\sin\theta=0}\)
par le théorème du moment cinétique par rapport au pivot du pendule:
\(\displaystyle{\frac{\textrm d}{\textrm{dt}}(\overrightarrow{OM}\wedge m\overrightarrow v)=\overrightarrow{OM}\wedge(\overrightarrow T+\overrightarrow P)}\)
ce qui donne en fonction de la variable \(\theta\) :
\(\displaystyle{ml^2\ddot\theta=-mgl\sin\theta}\)
on aboutit de nouveau à \(\displaystyle{\ddot\theta+\frac{g}{l}\sin\theta=0}\)
Dans tous les cas, on obtient l'équation du mouvement du pendule que l'on sait intégrer dans l'hypothèse des petites oscillations, donc pour des angles \(q\) très petits tels que \(\displaystyle{\sin\theta\approx\theta}\):
\(\displaystyle{\ddot\theta+\frac{g}{l}\theta=0}\)
Remarque :
Une équation tout à fait semblable est obtenue pour le pendule de torsion (solide en rotation autour d'un axe et soumis à un couple de rappel) où \(J\) est le moment d'inertie et \(C\) la constante de torsion
\(\displaystyle{\ddot\theta+\omega_0^2\theta=0\textrm{ avec }\omega_0^2=\frac{C}{J}}\)