Dioptre plan

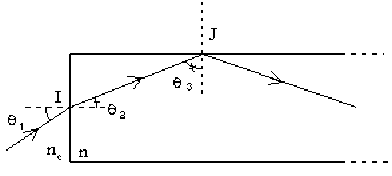
• Montrer qu'un rayon lumineux, entrant avec un angle quelconque par une des faces, subit une réflexion interne totale, dans la barre, lorsqu'il frappe les côtés.

Ecrivons la loi de la réfraction en \(I\) : \(n_e\sin\theta_1=n\sin\theta_2\) or \(\theta_3=\frac{\pi}2-\theta_2\).

Il y aura réflexion totale en \(J\) si \(\theta_3\ge\lambda\) avec \(\lambda\) tel que : \(n.\sin\lambda=n_e\) ; \(\sin\lambda=\frac{n_e}n\)

\(\theta_3\ge\lambda\Rightarrow\sin\theta_3\ge\sin\lambda\) (1 pt)

\(\sin\theta_3\ge\frac{n_e}n\) que l'on peut écrire sous la forme :

\(n.\sin\theta_3\ge n_e\Rightarrow n.\sin\left(\frac\pi2-\theta_2\right)\ge n_e\)

\(n.\cos\theta_2\ge n_e\) or \(\sin\theta_2=\frac{n_e}n.\sin\theta_1\) et donc :

\(\cos\theta_2=\sqrt{1-\frac{n^2_e}{n^2}.\sin^2\theta_1}\) d'où l'inégalité : \(n.\sqrt{1-\frac{n^2_e}{n^2}.\sin^2\theta_1}\ge n_e\) (1 pt)

soit : \(n^2-n^2_e.\sin^2\theta_1\ge n^2_e\) ou en définitive : \(n^2\ge n^2_e(1+\sin^2\theta_1)\). la valeur maximum de

\((1+\sin^2\theta_1)\) est 2 et donc il y a réflexion totale interne pout tout \(\theta_1\) si : \(n^2\ge2n^2_e\) soit : \(n\ge\sqrt2n_e\)

si \(n = 1,54\) et \(ne = 1\) (indice de l'air) alors \(\sqrt2n_e=1,44\) et \(n>\sqrt2n_e\) ce qui entraîne qu'il y aura réflexion totale interne quel que soit l'angle d'incidence \(\theta_1\). (1 pt)

• Que se passerait-il si elle se trouvait dans l'eau ?

Mais dans l'eau \(n_e=1,33\) et \(\sqrt2n_e=1,88\) qui est plus grand que n. Il n'y aura réflexion interne totale que si :

\(\sin^2\theta_1\le\frac{n^2}{n^2_e}-1=0,34 l\) soit \(\theta_1\le35,7°\) (2 pts)