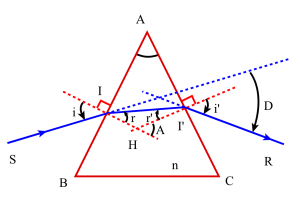
Marche d'un rayon monochromatique
Considérons un prisme défini dans son plan de section principale par son angle A et son indice relatif n>1. On rappelle que par hypothèse, le milieu ambiant est l'air.
Soit SI un rayon incident quelconque qui frappe en I la face d'entrée AB du prisme ; provenant d'un milieu moins réfringent que celui du prisme, ce rayon subit en I le phénomène de réfraction en respectant les deux lois de Descartes.
Simuler
L'animation suivante illustre la marche d'un rayon lumineux à travers la section principale d'un prisme :
On a donc, si II' représente le rayon transmis, la relation : \(\sin~i=n~\sin~r~~~~(1)\)
Supposons qu'en I', les conditions angulaires soient telles qu'elles permettent l'émergence du rayon lumineux suivant I'R. Dans ces conditions on peut écrire que: \(\sin~i'=n~\sin~r'~~~~(2)\)
Compte tenu de la définition du prisme, il est clair que le rayon émergent ne peut être dans le prolongement du rayon incident, pas plus qu'il ne peut lui être parallèle. Le prisme a donc bien le pouvoir de dévier la lumière, et cette déviation a pour effet dans le cas général, de rabattre vers la base BC du prisme le rayon lumineux.
L'angle de déviation D est par définition l'angle dont il faut faire tourner le rayon incident SI pour l'amener dans la direction du rayon émergent I'R. Cette déviation est donc la somme de deux déviations successives qui ont lieu dans le même sens, l'une à l'entrée, l'autre à la sortie du prisme, soit : \(D=(i~-~r)~+~(i'~-~r')\)
Cette relation peut être exprimée différemment car dans le triangle IHI' l'angle extérieur en H, égal à r + r' , a ses cotés perpendiculaires à ceux de l'angle A. Par suite : \(A=r~+~r'~~~~(3)\) ce qui entraîne : \(D=i~+~i'-~A~~~~(4)\)
Attention :
On notera que les relations (1), (2) , (3) et (4) sont généralisables à tous les cas de figure, à condition de définir algébriquement les angles, de la façon suivante :
- i et r sont comptés positifs, s'ils sont décrits à partir de la normale à la face d'entrée AB dans le sens trigonométrique.
- i' et r' le sont également si, à partir de la normale à la face de sortie AC, ils sont décrits dans le sens inverse, c'est-à-dire rétrograde.
- D est quant à lui compté positivement si, partant de la direction du rayon incident, on le décrit dans le sens rétrograde.
Les formules du prisme se résument de la façon suivante :
\(\sin~\mathrm i=\mathrm n~\sin~\mathrm r\)
\(\sin~\mathrm{i'}=\mathrm n~\sin~\mathrm{r'}\)
\(\mathrm r+\mathrm r'=\mathrm A\)
\(\mathrm D=\mathrm i+\mathrm{i'}-\mathrm A\)