Prisme de petit angle
Partie
Question
Retrouver la relation de conjugaison, dans l'air, des lentilles minces,
\(-\frac1p+\frac1{p'}=\frac1{f'}=(n-1)\cdot\left(\frac1{R_1}-\frac1{R_2}\right)\)(2), c'est-à-dire \(-\frac1{\overline{SO}}+\frac1{\overline{SI}}=(n-1).\left(\frac1{\overline{SC_1}}-\frac1{\overline{SC_2}}\right)\), en utilisant la déviation, dans l'air, par les prismes de petit angle : \(D=(n-1).\hat{A}\)(1).
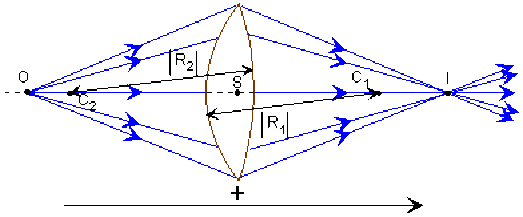
Décomposer la section de la lentille en morceaux de prisme.
Aide simple
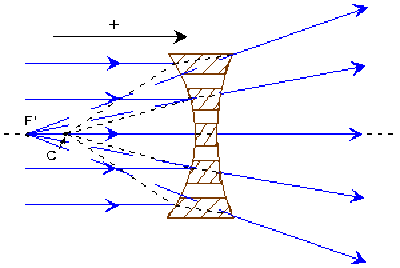
La section droite d'une lentille peut être considérée comme un ensemble de morceaux de prismes superposés dont l'angle au sommet \(A\) est petit et varie d'une manière continue du centre à la périphérie.
La section périphérique de la lentille a le plus grand angle A. La section centrale est équivalente à une lame à face parallèle c'est-à-dire à un prisme d'angle \(A\) nul \((\hat{A}=0)\).
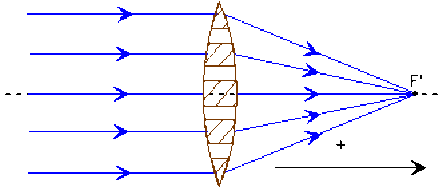
La déviation de la lumière par un prisme de petit angle, proportionnelle à son angle \(A\) explique la convergence (ou divergence) accrue des rayons incidents à la périphérie d'une lentille mince et la formation d'un foyer.
Aide détaillée
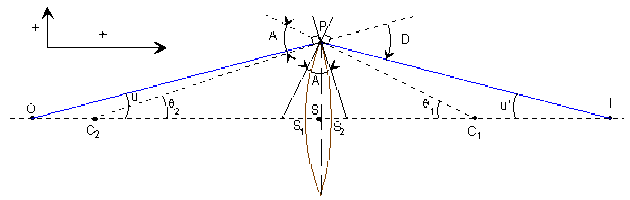
La déviation par un prisme est la somme des déviations par deux dioptres plans. Le rayon incident \(OP\) issu du point objet \(O\) de l'axe, se réfracte en \(P\) sur chacun des dioptres de sommet \(S_1, S_2\) et subit une déviation \(D\) pour former une image en \(I\) du point \(O\) avec le rayon perpendiculaire aux 2 dioptres, non dévié, de direction \(OS\).
Les triangles \(OPI\) et \(C_2PC_1\) permettent d'exprimer les angles de déviation \(D\) et l'angle \(A\) du prisme équivalent à la lentille mince au point \(P\).
\(D=u+u'A=q_1+q_2\)
Rappel de cours
Tout rayon passant par le centre optique d'une lentille mince n'est pas dévié.
Tout rayon incident parallèle à l'axe principal émerge de la lentille en passant par le foyer principal image.
Tout rayon incident passant par le foyer objet émerge de la lentille parallèlement à l'axe principal.
Pour une lentille sphérique mince, il existe deux plans focaux symétriques par rapport à la lentille: le plan focal objet et le plan focal image. Ces plans comme les foyers qui les forment sont réels pour une lentille convergente et virtuels pour une lentille divergente.
Une lentille mince est optiquement définie par sa distance focale.
Les relations de conjugaison :
origine au centre
\(-\frac1{\overline{OA}}+\frac1{\overline{OA'}}=\frac1{f'}\)
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OA'}}{\overline{OA}}=\frac{p'}p\)
origine aux foyers
\(\overline{FA}=x\) et \(\overline{F'A'}=x'\)
\(x\cdot x'=-f'^2\)
\(\gamma=\frac{f'}x=-\frac{x'}{f'}\)
Solution détaillée
Pour une lentille mince, on peut considérer que \(S_1, S_2, S\) et \(H\) sont confondus. D'où :
\(A=\theta_1+\theta_2\#\frac{\overline{SP}}{\overline{SC_1}}+\frac{\overline{SP}}{-\overline{SC_2}}\)(1) \(D=u+u'=\frac{\overline{SP}}{-\overline{SO}}+\frac{\overline{SP}}{\overline{SI}}\)(2)
Soit en divisant (1) et (2) par \(\overline{SP}\) et en écrivant \(D = (n-1).A\) :
\(\frac D{\overline{SR}}=-\frac1{\overline{SO}}+\frac1{\overline{SI}}=(n-1)\cdot\left(\frac1{\overline{SC_1}}-\frac1{\overline{SC_2}}\right)\)