Convention d'écriture des nombres [Systèmes et unités de mesures]

Convention d'écriture des nombres

Règles

Les nombres s'écrivent avec des chiffres arabes en caractères romains (droits).
Exemples : $2 ~54 ~730$

Pour les nombres à partie décimale, la virgule (et non le point) sépare la partie entière de la partie décimale.
Exemples : $\mathrm{0,024}$ $\mathrm{1,35}$ $\mathrm{679,8}$

Si un nombre a plus de quatre chiffres chaque groupe de trois chiffres, doit être séparé par un espace.
Exemples : $6545$ ou $6~545$ ; $72~840$ ; $1~459~362$
La séparation n'existe pas pour les nombres de quatre chiffres désignant une date ou un millésime (l'an 2000).

Pour un nombre avec parties entière et décimale, la séparation se fait de part et d'autre de la virgule.
Exemples : $\mathrm{0,078 ~65}$ ; $\mathrm{1~432,315 ~8}$

Puissance de 10

Les grands et les petits nombres peuvent s'exprimer à l'aide des puissances de $10$ . En notation "scientifique", un chiffre différent de zéro se trouve devant la virgule.
Exemples : $12~400 = \mathrm{1,24} \times 10^{4}$ ; $\textrm{0,000 034 27} = \mathrm{3,427} × 10^{-5}$
En notation "ingénieur", l'exposant est un multiple de $3$ .
Exemples : $12~400 = \mathrm{12,4} \times 10^{3}$ ; $\textrm{0,000 034 27} = \mathrm{34,27} \times 10^{-6}$

Les nombres dont les noms sont terminés par "illion" sont à éviter, par risque de confusion, sauf million qui vaut $10^{6}$ . En effet la formulation diffère suivant les pays :

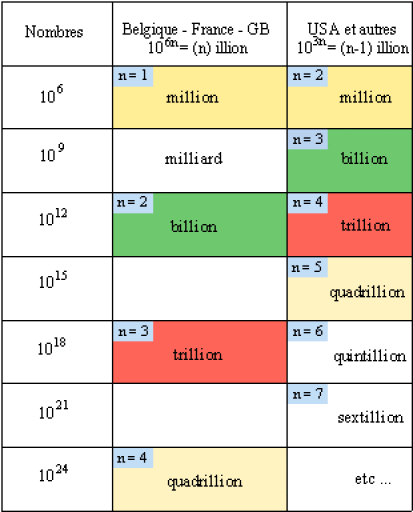
Signes d'opération

Addition - Soustraction : utilisation des signes usuels $"+"$ et $"-"$ .
Exemple : $(5 + 2) - (15 + 3)$

Multiplication : utiliser le signe $"\times"$ . Ne pas utiliser la lettre $\textrm{x}$ , l'astérisque $*$ , le point multiplicatif $\cdot$ (sauf devant une puissance de $10$ ).
Exemples : $4 \times \mathrm{23,4} \times 13~470$ ; $\mathrm{3,24} × 2 × 10^{4}$ ou $\mathrm{3,24} \times 2 \cdot 10^{4}$ .

Division : utiliser la barre horizontale $(-)$ ou la barre oblique $( / )$ .
Exemples : $\frac{12\times \mathrm{7,47}}{1,6\times10^4\times4522}=(12\times \mathrm{7,47})/(\mathrm{1,6}\times10^4\times4522)$

Les chiffres significatifs

La précision d'une mesure d'un phénomène physique se traduit dans l'expression du résultat par le nombre de chiffres dits "significatifs".
Exemples : la mesure $m = \mathrm{125,7} \textrm{ g}$ (quatre chiffres significatifs) indique une mesure de la masse avec une précision au $1/10$ de gramme. C'est au milligramme près si le résultat est exprimé par $m' = \mathrm{125,700} \textrm{ g}$ avec 6 chiffres significatifs.

Les chiffres significatifs sont :
- les chiffres différents de zéro.
- les zéros placés entre les chiffres.
- les zéros placés derrière les autres chiffres quand ils sont le résultat de la mesure.
Exemples : les chiffres significatifs sont en gras
2 ; 45 ; 0,203 ; 0,004 57
7,30 × 10³ ; 40,700 × 10⁶
42 300 environ ou 423 × 10⁶
300 m (mesuré au m près)
600 000 habitants environ
600 000 habitants exactement

Présentation du résultat d'une mesure
Un résultat de mesure de $\mathrm{42,3} \textrm{ cm}$ (trois chiffres significatifs) suggère l'intervalle de certitude suivant : $\mathrm{42,25} \textrm{ cm} \leq \mathrm{42,3} \textrm{ cm} \leq \mathrm{42,35} \textrm{ cm}$ .
Si des mesures expérimentales ont conduit aux résultats suivants : $\mathrm{42,27}\textrm{ cm}$ - $\mathrm{42,45}\textrm{ cm}$ - $\mathrm{42,72}\textrm{ cm}$ avec trois chiffres significatifs, nous obtenons respectivement : $\mathrm{42,3}\textrm{ cm}$ - $\mathrm{42,5}\textrm{ cm}$ et $\mathrm{42,7}\textrm{ cm}$ suivant la règle :

Règle :

On arrondit par défaut si le premier chiffre supprimé est inférieur à $5$ et par excès s'il est supérieur ou égal à $5$ .

Détermination du nombre de chiffres significatifs dans les opérations résultats de mesures.
On distingue les cas suivants :
- Addition - Soustraction^[1]
- Multiplication - Division^[2]
- Puissance - Racine^[3]

Coefficients numériques

La multiplication ou la division par un coefficient numérique, doit conduire à un résultat avec un chiffres significatifs, comparable à celui du résultat de la mesure qui en possède le moins.
Exemples :
- Pour un résultat de mesure de $\mathrm{31,2}$ $(n = 3)$ nous obtenons :
  $3 \times \mathrm{31,2} = \mathrm{93,6} ~(n = 3)$
  $4 \times \mathrm{31,2} = \mathrm{124,8}~ (n + 1 = 4)$ car le dernier produit $(4 \times 3)$ est supérieur à $9$ .
- La moyenne de plusieurs résultats de mesures conduit à :
  $M=\frac{42,39+42,1+42,732}{3}=\frac{127,222}{3}$
  donc $M = \textrm{42,407 333}$ arrondi à $42,4$
Dans le cas d'opérations avec les nombres transcendants $(\pi)$ et $(e)$ , leurs expressions dans les calculs dépendront des chiffres significatifs des résultats de mesures.
Exemples :
- Cas de $\pi = \textrm{3,141 592 7...}$
  Dans l'opération $\frac{\textrm{4,135~7}\times \textrm{1,203}}{\pi}$ où le plus petit nombre de chiffres significatifs est $n = 4$ , nous prenons $\pi = \textrm{3,141 6}$ , d'où $\frac{\textrm{4,135~ 7} \times \textrm{1,203}}{\textrm{3,141~6}}=1,583~666~6$
  arrondi à $\mathrm{1,584}$ .
  On donne le rayon $(R = \textrm{1,15 cm})$ et la hauteur $(h = \textrm{2,5 cm})$ d'un cône de révolution. Le volume de ce cône est calculé en prenant : $\pi = \mathrm{3,14}$ car $n = 2$ pour la hauteur, d'où $V=\frac{1}{3}\pi R^2h=\frac{1}{3}\times3,14\times(1,15)^2\times2,5$
  donc $V = \textrm{3,460 541 7}$ arrondi à $\textrm{3,5 cm}^{3}$ .
- Cas de $e = \textrm{2,718 281 8...}$
  Pour la multiplication : $\textrm{3,05} \times e$ nous prenons $e = \textrm{2,718}$ d'où $\textrm{3,05} \times \textrm{2,718} = \textrm{8,289 9}$ arrondi $\mathrm{8,29}$ .
  La décharge d'un condensateur, initialement chargé de $q_{0}= \textrm{7,45 C}$ , suit la loi : $q(t)=q_0~e^{-t/\tau}$ ( $\tau$ : constante de temps)
  A, $t = \tau$ , la charge du condensateur sera : $q(\tau)=q_0e^{-1}=\frac{q_0}{e}=\frac{7,45e}{2,718}=\textrm{2,740~986 C}$ arrondi à $\textrm{2,74 C}$
  La précision d'un résultat, n'est pas corrélée au nombre maximum de chiffres après la virgule, obtenu par une calculatrice électronique.

Notes

Addition - Soustraction
Les résultats de mesures sont des nombres entiers :
on effectue les opérations habituelles de somme et de différence :
Exemples : $45 \textrm{ cm} + 251 \textrm{ cm} = 296 \textrm{ cm} ; 1345 \textrm{ g} - 923 \textrm{ g} = 422 \textrm{ g}$
Les résultats de mesures sont des nombres avec chiffres décimaux :
Le résultat de l'opération dépend du nombre de chiffres significatifs après la virgule.
Parmi les résultats de mesures, considérer celui qui possède le plus petit nombre de chiffres significatifs après la virgule : soit n ce nombre
- Arrondir tous les autres nombres à $( n+1)$ chiffres après la virgule.
- Effectuer les opérations d'addition ou de soustraction.
- Arrondir le résultat à n chiffres après la virgule.
Exemples :
Cas de l'addition :
$S = \textrm{12,452 7} + \mathrm{4,37} + \mathrm{450,321} + \mathrm{21,145}$ $( n = 2)$
$S = \mathrm{12,452} + \mathrm{4,37} + \mathrm{450,321} + \mathrm{21,145}$
$S = \mathrm{488,289}$ arrondi à $\mathrm{488,29}$
Cas de la soustraction :
$D = \mathrm{4,3} - \textrm{1, 245 2} = \mathrm{4,3} - \mathrm{1,24} = \mathrm{3,05}$ arrondi à $\mathrm{3,1}$
Les résultats de mesures exprimés à l'aide de puissance positives de $10$ .
Ramener tous les résultats de mesures en fonction de la plus haute puissance de $10$ avant de procéder à la démarche précédente.
Exemples :
Cas de l'addition :
$S = \mathrm{3,1} \times 10^{3} + \mathrm{5,46} \times 10^{4} + \mathrm{7,8} \times 10^{5}$
$S = \mathrm{0,031} \times 10^{5} + \mathrm{0,546} \times 10^{5} + \mathrm{7,8} \times 10^{5} \quad (n = 1)$
$S = \mathrm{0,03} \times 10^{5} + \mathrm{0,55} \times 10^{5} + 7,8 \times 10^{5}$
$S = \mathrm{8,38} \times 10^{5}$ arrondi à $\mathrm{8,4} \times 10^{5}$
Cas de la soustraction :
$D = \mathrm{4,75} \times 10^{5} - \mathrm{2,156} \times 10^{3}$
$D = \mathrm{4,75} \times 10^{5} - \textrm{0,021 56} \times 10^{5}$
$D = \mathrm{4,75} \times 10^{5} - \mathrm{0,022} \times 10^{5}$
$D = \mathrm{4,728} \times 10^{5}$ arrondi à $\mathrm{4,73} \times 10^{5}$
Multiplication - Division
Le résultat de l'opérateur dépend du nombre total de chiffres significatifs
Dans les résultats de mesures, considérer celui qui possède le plus petit nombre de chiffres significatifs : soit $n$ ce nombre.
- Arrondir tous les autres nombres à $(n+1)$ chiffres.
- Effectuer les opérations de multiplication ou de division.
- Arrondir le résultat pour la multiplication à :
  $(n)$ chiffres si la dernière somme partielle est inférieure à $9$ .
  $(n+1)$ chiffres si la dernière somme partielle est supérieure à $9$ .
Exemples :
Cas de la multiplication :
math.param [param]
Cas de la division :
$\frac{\mathrm{41,454}}{\mathrm{1,6}} = \frac{\mathrm{41,5}}{\mathrm{1,6}} = \textrm{25,937 5}$ arrondi à $26$
$\frac{\mathrm{414,456}}{\mathrm{2,18}} = \frac{\mathrm{414,6}}{\mathrm{2,18}} = \textrm{190,183}$ arrondi à $190$
Puissance - Racine
La réponse doit contenir autant de chiffres significatifs que la grandeur mesurée, sauf si cette puissance ou cette racine, intervient dans une opération; auquel cas on augment d'unité le nombre de chiffres significatifs de résultat.
Exemples :
Cas d'une puissance :
$(\mathrm{5,275})2 = \textrm{27,825 625}$ arrondi à $\mathrm{27,83}$
$(\mathrm{5,275})5 = \mathrm{4084,25}$ arrondi à $\mathrm{4,084} \times 10^{3}$
Cas d'une racine :
$\sqrt{52,75} = \textrm{7,262 919 5}$ arrondi à $\mathrm{7,263}$
$\sqrt[5]{\mathrm{5,27}} = \textrm{1,394 318 9}$ arrondi à $\mathrm{1,39}$