Vecteurs de Fresnel
Définition :
On associe à une grandeur sinusoïdale du temps \(s(t) = S \cos(\omega t + \varphi)\) un vecteur \(\overrightarrow{OM}\) appelé vecteur de Fresnel :
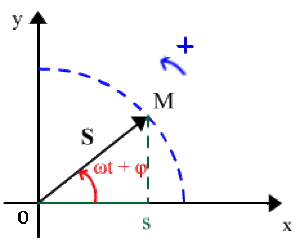
de module constant \(\Big\Arrowvert \overrightarrow{OM} \Big\Arrowvert = S\)
tournant dans le sens trigonométrique à la vitesse angulaire \(\omega\)
d'angle orienté \(\Big(\overrightarrow{Ox},\overrightarrow{OM}\Big)\) à l'instant t et de mesure \((\omega t + \varphi)\)
La projection du vecteur \(\overrightarrow{OM}\) sur l'axe \(Ox\) représente la grandeur sinusoïdale :
\(s(t) = S \cos(\omega t + \varphi)\)
Propriétés
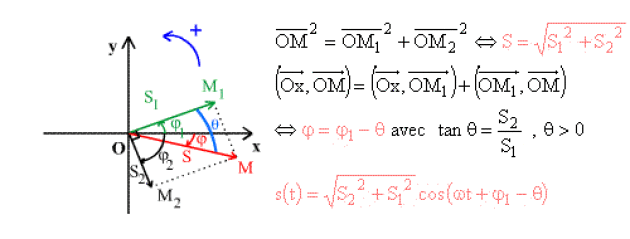
Le vecteur de Fresnel \(\overrightarrow{OM}\) associé à la somme \(s(t)\) de deux fonctions sinusoïdales \(s_1(t)\) et \(s_2(t)\) est la somme des vecteurs de Fresnel \(\overrightarrow{OM_1}\) et \(\overrightarrow{OM_2}\) associés à chacune de ces fonctions.
Propriétés du vecteur \(\overrightarrow{OM}\) : associons à
la vibration \(s_1(t) = S_1 cos(\omega t + \varphi_1)\) le vecteur tournant \(\overrightarrow{OM_1}\)
\(\Big\Arrowvert\overrightarrow{OM_1} \Big\Arrowvert= S_1\); \(\Big(\overrightarrow{Ox},\overrightarrow{OM_1} \Big) = \omega t + \varphi_{1}\); \(\overline{Om_1} = S_1 \cos (\omega t + \varphi_1 ) = s_1(t)\)
la vibration \(s_2(t) = S_2 cos(\omega t + \varphi_2)\) le vecteur tournant \(\overrightarrow{OM_2}\)
\(\Big\Arrowvert \overrightarrow{OM_2} \Big\Arrowvert= S_2\); \(\Big(\overrightarrow{Ox},\overrightarrow{OM_2} \Big) = \omega t + \varphi_{2}\); \(\overline{Om_2} = S_2 \cos (\omega t + \varphi_2 ) = s_2(t)\)
la vibration résultante \(s(t) = s_1(t) + s_2(t) = S \cos(\omega t + \varphi)\) le vecteur tournant
\(\overrightarrow{OM} = \overrightarrow{OM_1} + \overrightarrow{OM_2}\)
\(\Big\Arrowvert\overrightarrow{OM} \Big\Arrowvert= S\); \(\Big(\overrightarrow{Ox},\overrightarrow{OM} \Big) = \omega t + \varphi\); \(\overline{Om} = S \cos (\omega t + \varphi ) = s(t)\)
Cas général
Représentation graphique de \(\overrightarrow{OM}\):
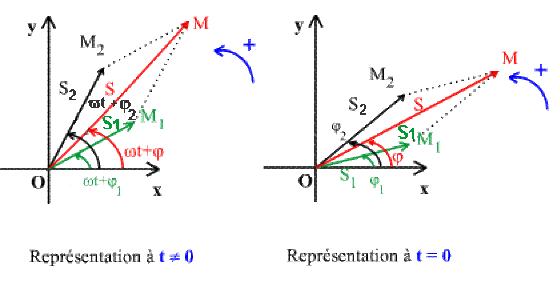
Détermination graphique de \(S\) et \(\varphi\) (Représentation à \(t = 0\))
Cas où \(S_1\ne S_2\) : \(OM_1\) \(MM_2\) est un parallélogramme
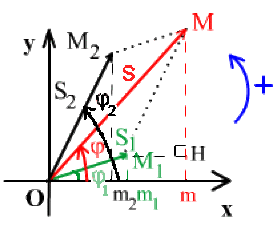
Dans le triangle \(OMm\), nous avons :
\(\overline{mM} = \overline{mH} + \overline{HM} = \overline{m_1M_1} + \overline{m_2M_2}\)
\(\overline{Om} = \overline{Om_1} + \overline{m_1m} = \overline{Om_1} + \overline{Om_2}\)
d'où \(\tan \varphi = \frac{\overline{mM}}{\overline{Om}} = \frac{S_{1} \sin \varphi_{1} + S_{2} \sin \varphi_{2}}{S_{1} \cos \varphi_{1} + S_{2} \cos \varphi_{2}}\)
et
\(\begin{array}{ll} S^{2} &= {\overline{OM}}^{2} = {\overline{Om}}^{2} + {\overline{mM}}^{2} \\ &= \Big(S_{1} \cos \varphi_{1} + S_{2} \cos \varphi_{2}\Big)^{2} + \Big(S_{1} \sin \varphi_{1} + S_{2} \sin \varphi_{2}\Big)^{2} \end{array}\)
\(S^{2} = S_{1}^{2} + S_{2}^{2} + 2S_{1}S_{2} \cos(\varphi_{2} - \varphi_{1})\)
Exemple : Somme de deux signaux sinusoïdaux d'amplitudes différentes
Construire le vecteur associé à la grandeur sinusoïdale \(s(t) = S \cos(\omega t + \varphi)\), somme de deux signaux sinusoïdaux \(s_1(t) = \cos(\omega t + \pi/6)\)
et \(s_2(t) = 2 \cos(\omega t + \pi/3)\) . En déduire les valeurs de \(S\) et \(\varphi\).
Représentons les vecteurs de Fresnel à \(t = 0\)
La vibration \(s_1(t)\) est représentée par le vecteur tournant \(\overrightarrow{OM_1}\)
\(\Big\Arrowvert\overrightarrow{OM_1} \Big\Arrowvert = 1 ; \Big(\overrightarrow{Ox} , \overrightarrow{OM_1}\Big) = \frac{\pi}{6}\)
La vibration \(s_2(t)\) est représentée par le vecteur tournant \(\overrightarrow{OM_2}\)
\(\Big\Arrowvert\overrightarrow{OM_2} \Big\Arrowvert = 2 ; \Big(\overrightarrow{Ox} , \overrightarrow{OM_2}\Big) = \frac{\pi}{3}\)
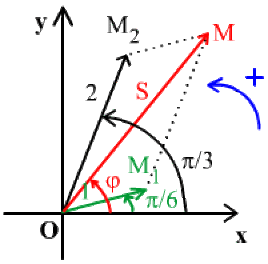
La construction du parallélogramme \(OM_1\) \(MM_2\) permet la mesure "approximative" de
\(S = OM ~\#~ 3\) et \(\varphi = \Big(\overrightarrow{Ox} , \overrightarrow{OM}\Big) ~\#~ 50^{\circ}\)
Valeurs de \(S\) et \(\varphi\) calculées
\(\begin{array}{ll} S & = \Big[S_{1}^{2} + S_{2}^{2} + 2S_{1}S_{2} \cos(\varphi_{2} - \varphi_{1}) \Big]^{1/2} \\ &= \Big[1^2 + 2^2 + 2 \times 1 \times 2 \cos \frac{\pi}{6} \Big]^{1/2} = \Big[5 + 2 \sqrt{3} \Big]^{1/2} \\ &\# ~ 2,91 \end{array}\)
\(\begin{array}{ll} \varphi & = \textrm{Arctan } \frac{S_{1} \sin \varphi_{1} + S_{2} \sin \varphi_{2}}{ S_{1} \cos \varphi_{1} + S_{2} \cos \varphi_{2}} = \textrm{Arctan } \frac{1 + 2 \sqrt{3}}{2 + \sqrt{3}} \\ &\# ~50^{\circ},10 \end{array}\)
Cas où \(S_1 = S_2 = S_0\) : \(OM_1\) \(MM_2\) est un losange
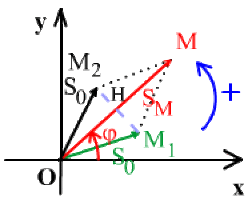
\(\varphi = \frac{(\varphi_{1}+ \varphi_{2})}{2}\) et \(S = OM = 2OH = 2S_0 \cos \frac{\varphi_2 - \varphi_1}{2}\)
et \(s(t) = 2 S_0 \cos \frac{\varphi_2 - \varphi_1}{2} \cos \Bigg(\omega t + \frac{\varphi_2 + \varphi_1}{2} \Bigg)\)
Ce résultat peut être obtenu par les formules précédentes en remplaçant \(S_1\) et \(S_2\) par \(S_0\). En effet
\(\tan \varphi = \frac{\sin \varphi_{1} + \sin \varphi_{2}}{\cos \varphi_{1} + \cos \varphi_{2}} = \frac{2 \sin \frac{\varphi_{1} + \varphi_{2}}{2} \cos \frac{\varphi_{1} - \varphi_{2}}{2}}{2 \cos \frac{\varphi_{1} + \varphi_{2}}{2} \cos\frac{\varphi_{1} - \varphi_{2}}{2}} = \tan \frac{\varphi_{1} + \varphi_{2}}{2}\)
\(\Leftrightarrow ~\varphi = \frac{(\varphi_{1} + \varphi_{2})}{2}~ \Big[\pi\Big]\)
et \(S^{2} = 2 S_{0}^{2} (1 + \cos(\varphi_{2} - \varphi_{1})) = 4 S_{0}^{2} \cos^{2} \frac{\varphi_{2} - \varphi_{1}}{2}\)
\(\Leftrightarrow \arrowvert S \arrowvert = 2 S_{0} \left\arrowvert \cos \frac{\varphi_{2} - \varphi_{1}}{2}\right\arrowvert\)
Exemple : Somme de deux signaux sinusoïdaux de même amplitude
Construire le vecteur associé à la grandeur sinusoïdale \(s(t) = S \cos(\omega t + \varphi)\), somme de deux signaux sinusoïdaux \(s_1(t) = 2 cos(\omega t + \pi/6)\) et \(s_2(t) = 2 \cos(\omega t + \pi/3)\) . En déduire les valeurs de \(S\) et \(\varphi\).
Représentons les vecteurs de Fresnel à \(t = 0\)
La vibration \(s_1(t)\) est représentée par le vecteur tournant \(\overrightarrow{OM_{1}}\)
\(\Big\Arrowvert \overrightarrow{OM_{1}} \Big\Arrowvert = 2 ; \Big(\overrightarrow{Ox},\overrightarrow{OM_{1}}\Big) = \frac{\pi}{6}\)
La vibration \(s_2(t)\) est représentée par le vecteur tournant \(\overrightarrow{OM_{2}}\)
\(\Big\Arrowvert \overrightarrow{OM_{2}} \Big\Arrowvert = 2 ; \Big(\overrightarrow{Ox},\overrightarrow{OM_{2}}\Big) = \frac{\pi}{3}\)
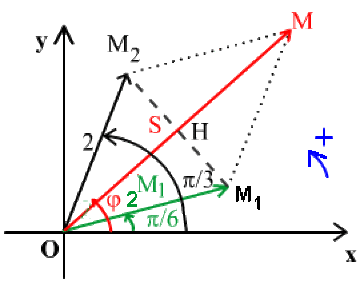
La construction du losange \(OM_1\) \(MM_2\) permet la mesure "approximative" de
\(S = OM ~\# ~ 3,8\) et \(\varphi = \Big(\overrightarrow{Ox},\overrightarrow{OM}\Big)~ \# ~45^{\circ}\)
Valeurs de \(S\) et \(\varphi\) calculées
\(S = 2 OH = 2 S_{0}~ \cos \frac{\varphi_{2} - \varphi_{1}}{2} = 2 \times 2 \times \cos \frac{\pi}{12} ~\#~3,86\)
\(\varphi = \frac{\varphi_{2} + \varphi_{1}}{2} = \frac{\pi}{4}\)
Cas particuliers
Vibration en phase
\(\varphi_{1} = \varphi_{2} = \varphi_{0}\)
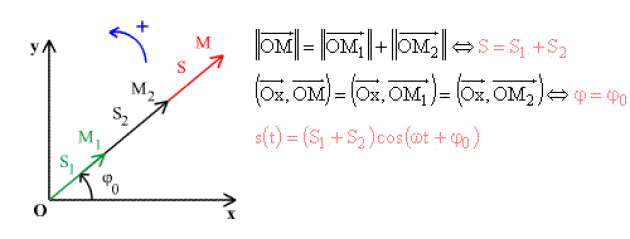
Vibration en oppposition de phase
\(\varphi_{2} = \varphi_{1} + \pi\)
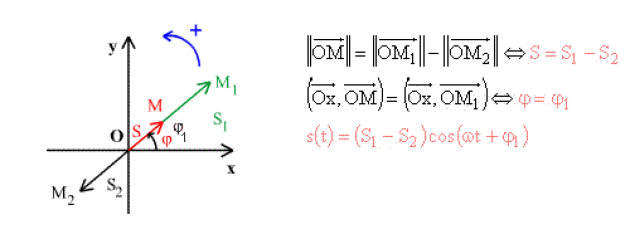
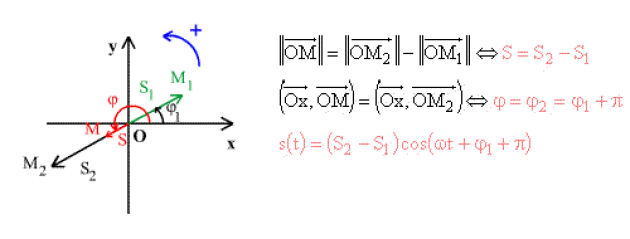
Vibration en quadrature de phase
\(\varphi_{2} = \varphi_{1} \pm \pi / 2\)
Cas où \(M_2\) est en avance sur \(M_1\) : \(\varphi_2 = \varphi_1 + \pi /2\)
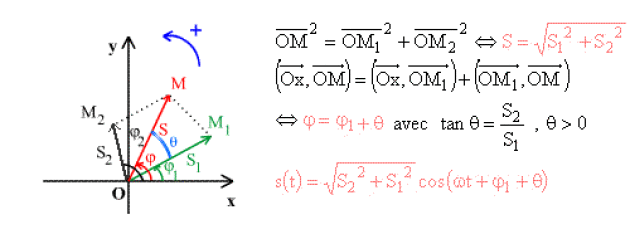
Cas où \(M_2\) est en retard sur \(M_1\) : \(\varphi_2 = \varphi_1 - \pi /2\)