Produit scalaire
Partie
Question
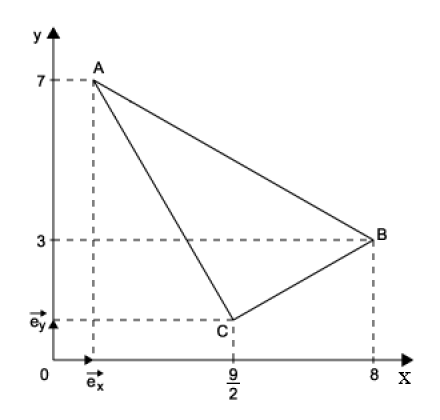
Dans un repère cartésien orthonormé \(\Big(O;\overrightarrow{e_{x}}, \overrightarrow{e_{y}}\Big)\),on donne les trois points \(A(1,7) ;B(8,3)\) et \(C\Bigg(\frac{9}{2}, 1 \Bigg)\) formant le triangle \(ABC\).
Déterminer les composantes et les normes des vecteurs \(\overrightarrow{AB}\), \(\overrightarrow{AC}\) et \(\overrightarrow{BC}\).
Aide simple
Utiliser la relation de Chasles pour les composantes et le théorème de Pythagore pour les modules.
Aide détaillée
Relation de Chasles : \(\overrightarrow{AB} = \overrightarrow{AO} + \overrightarrow{OB} = \overrightarrow{OB} - \overrightarrow{OA}\)
Théorème de Pythagore : \(\Big\Arrowvert \overrightarrow{AB} \Big\Arrowvert = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}}\)
Solution simple
Par application de la relation de Chasles ,successivement aux trois vecteurs,
Nous obtenons :
\(\overrightarrow{AB} = (7,-4); ~\overrightarrow{AC} = (\frac{7}{2},-6) ; ~\overrightarrow{BC} = (-\frac{7}{2},-2)\)
et pour les modules :
\(\Big\Arrowvert \overrightarrow{AB} \Big\Arrowvert = \sqrt{65} ~;~ \Big\Arrowvert \overrightarrow{AC} \Big\Arrowvert = \frac{\sqrt{193}}{2} ~;~ \Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert = \frac{\sqrt{65}}{2}\)
Solution détaillée
Application de la relation de Chasles pour les composantes :
\(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} =\left(\begin{array}{c} 8 \\\\ 3 \end{array} \right) - \left(\begin{array}{c} 1 \\\\ 7 \end{array} \right) = \left(\begin{array}{c} 7 \\\\ -4 \end{array} \right) \Leftrightarrow \overrightarrow{AB} = 7 ~\overrightarrow{e_{x}} - 4~\overrightarrow{e_{y}}\)
\(\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} =\left(\begin{array}{c} \frac{9}{2} \\\\ 3 \end{array} \right) - \left(\begin{array}{c} 1 \\\\ 7 \end{array} \right) = \left(\begin{array}{c} \frac{7}{2} \\\\ -6 \end{array} \right) \Leftrightarrow \overrightarrow{AC} = \frac{7}{2} ~\overrightarrow{e_{x}} - 6~\overrightarrow{e_{y}}\)
\(\overrightarrow{BC} = \overrightarrow{OC} - \overrightarrow{OB} =\left(\begin{array}{c} \frac{9}{2} \\\\ 3 \end{array} \right) - \left(\begin{array}{c} 8 \\\\ 3 \end{array} \right) = \left(\begin{array}{c} -\frac{7}{2} \\\\ -2 \end{array} \right) \Leftrightarrow \overrightarrow{BC} = -\frac{7}{2} ~\overrightarrow{e_{x}} - 2~\overrightarrow{e_{y}}\)
Normes (ou modules) de ces vecteurs :
\(\Big\Arrowvert \overrightarrow{AB} \Big\Arrowvert = \sqrt{(7)^{2} + (-4)^{2}} = \sqrt{65} \approx \mathrm{8,06}\)
\(\Big\Arrowvert \overrightarrow{AC} \Big\Arrowvert = \sqrt{\left(\frac{7}{2}\right)^{2} + (-2)^{2}} = \frac{\sqrt{193}}{2} \approx \mathrm{6,95}\)
\(\Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert = \sqrt{\left(-\frac{7}{2}\right)^{2} + (-6)^{2}} = \frac{\sqrt{65}}{2} \approx \mathrm{4,03}\)
Question
Dans un repère cartésien orthonormé \(\Big(O;\overrightarrow{e_{x}}, \overrightarrow{e_{y}}\Big)\),on donne les trois points \(A(1,7) ;B(8,3)\) et \(C\Bigg(\frac{9}{2}, 1 \Bigg)\) formant le triangle \(ABC\).
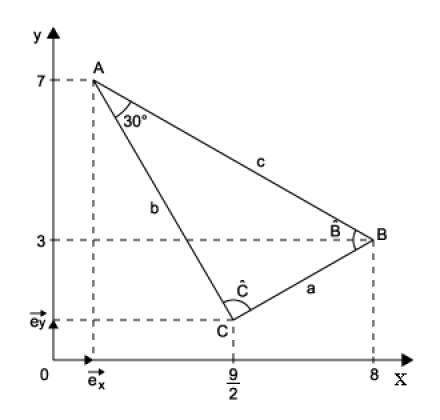
Par application d'une relation métrique dans un triangle quelconque ,calculer l'angle intérieur au sommet \(A\) du triangle \(ABC\)

Aide simple
Une relation métrique dans un triangle quelconque fait intervenir les carrés des cotés du triangle
Aide détaillée
Si \(a ,~b\) et \(c\) sont respectivement les modules des cotés opposés aux angles de sommets \(A ,~ B\) et \(C\) du triangle ,alors \(a^{2} = b^{2} + c^{2} - 2bc ~\cos \hat{A}\)
Solution simple
En appliquant la relation métrique ,nous trouvons :
\(\cos \hat{A} = \mathrm{0,86} \Leftrightarrow \hat{A} \approx 30^{\circ}\)
Solution détaillée
La relation métrique : \(a^{2} = b^{2} + c^{2} - 2bc ~\cos \hat{A}\)
Conduit à : \(\cos \hat{A} = \frac{b^{2} + c^{2} - a^{2}}{2bc}\)
avec
\(a^{2} = \Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert ^{2} = \frac{65}{4}\)
\(b^{2} = \Big\Arrowvert \overrightarrow{AC} \Big\Arrowvert ^{2} = \frac{193}{4}\)
\(c^{2} = \Big\Arrowvert \overrightarrow{AB} \Big\Arrowvert ^{2} = 65\)
d'où \(\cos \hat{A} = \frac{\frac{193}{4} + 65 - \frac{65}{4}}{2 \times \frac{\sqrt{193}}{2} \times \sqrt{65}} = \frac{388}{448} = \mathrm{0,866}\)
et \(\hat{A} \approx 30^{\circ}\)
Question
Dans un repère cartésien orthonormé \(\Big(O;\overrightarrow{e_{x}}, \overrightarrow{e_{y}}\Big)\),on donne les trois points \(A(1,7) ;B(8,3)\) et \(C\Bigg(\frac{9}{2}, 1 \Bigg)\) formant le triangle \(ABC\).
Exprimer la valeur de l'angle \(\hat{B}\) à partir de la définition du produit scalaire. En déduire l'angle \(\hat{C}\).
Aide simple
Le produit scalaire peut s'exprimer par une relation faisant intervenir le cosinus de l'angle
\(\hat{B} = (\overrightarrow{BA} , \overrightarrow{BC})\).
Aide détaillée
Par définition du produit scalaire de deux vecteurs \(\overrightarrow{BA}\) et \(\overrightarrow{BC}\) nous avons :
\(\overrightarrow{BA} \bullet \overrightarrow{BC} = \Big\Arrowvert \overrightarrow{BA} \Big\Arrowvert \Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert \cos (\overrightarrow{BA} , \overrightarrow{BC})\)
Solution simple
D'après la définition du produit scalaire des vecteurs \(\overrightarrow{BA}\) et \(\overrightarrow{BC}\) ,nous tirons :
\(\cos \hat{B} = \cos (\overrightarrow{BA} , \overrightarrow{BC}) = \frac{\overrightarrow{BA} \bullet \overrightarrow{BC}}{\Big\Arrowvert \overrightarrow{BA} \Big\Arrowvert \Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert} = \frac{33}{65} = \mathrm{0,507} \Leftrightarrow \hat{B} \approx 60^{\circ}\)
D'où \(\hat{C} = 180^{\circ} - (\hat{A} + \hat{B}) \Leftrightarrow \hat{C} \approx 90^{\circ}\)
Solution détaillée
D'après la définition du produit scalaire des deux vecteurs \(\overrightarrow{BA}\) et \(\overrightarrow{BC}\) nous tirons la valeur du \(\cos \hat{B}\).
\(\cos \hat{B} = \cos (\overrightarrow{BA} , \overrightarrow{BC}) = \frac{\overrightarrow{BA} \bullet \overrightarrow{BC}}{\Big\Arrowvert \overrightarrow{BA} \Big\Arrowvert \Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert}\)
avec : \(\overrightarrow{BA} \bullet \overrightarrow{BC} = \left(\begin{array}{c} -7 \\ +4 \end{array}\right)\bullet \left(\begin{array}{c} -\frac{7}{2} \\\\ -2 \end{array}\right) = \frac{49}{2} - 8 = \frac{33}{2}\) et
\(\Big\Arrowvert \overrightarrow{BA} \Big\Arrowvert \Big\Arrowvert \overrightarrow{BC} \Big\Arrowvert = \sqrt{65} \times \frac{\sqrt{65}}{2} = \frac{65}{2}\)
d'où \(\cos \hat{B} = \frac{33}{65} = \mathrm{0,507} \Leftrightarrow \hat{B} \approx 60^{\circ}\)
et \(\hat{C} = 180^{\circ} - (\hat{A} + \hat{B}) = 180^{\circ} - (30^{\circ} + 60^{\circ}) \Leftrightarrow \hat{C} \approx 90^{\circ}\)
Le triangle \(ABC\) est un demi triangle équilatéral .
Question
Dans un repère cartésien orthonormé \(\Big(O;\overrightarrow{e_{x}}, \overrightarrow{e_{y}}\Big)\),on donne les trois points \(A(1,7) ;B(8,3)\) et \(C\Bigg(\frac{9}{2}, 1 \Bigg)\) formant le triangle \(ABC\).
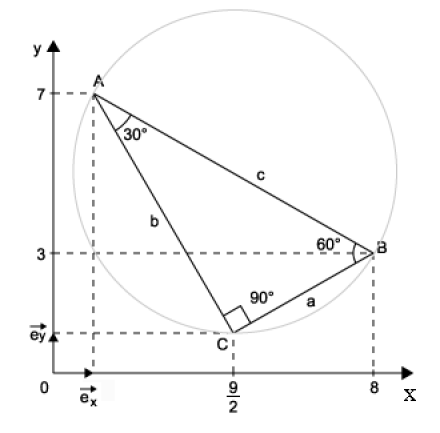
A partir du produit scalaire, retrouver l'équation cartésienne du cercle \((C_{0})\) de diamètre \(AB\) dans le plan \(xOy\) et vérifier, aux approximations prés, que le sommet \(C\) du triangle \(ABC\) appartient à ce cercle .
Aide simple
Pour un point \(M(x,y) \in C_{0}\),écrire une relation entre les vecteurs \(\overrightarrow{MA}\) et \(\overrightarrow{MB}\).
Aide détaillée
Si le point \(M(x,y) \in C_{0}\) alors les vecteurs \(\overrightarrow{MA}\) et \(\overrightarrow{MB}\) sont perpendiculaires et \(\overrightarrow{MA} \bullet \overrightarrow{MB} = 0\)
Solution simple
Pour un point \(M(x,y) \in C_{0}\) nous avons :
\(\overrightarrow{MA} \bullet \overrightarrow{MB} = 0 \Leftrightarrow x^{2} + y^{2} - 9x - 10y + 29 = 0\)
ou \(\left(x - \frac{9}{2} \right)^{2} + (y-5)^{2} = \left(\frac{\sqrt{65}}{2} \right)^{2}\)
Solution détaillée
Pour un point \(M(x,y) \in C_{0}\) nous avons :
\(\overrightarrow{MA} \bullet \overrightarrow{MB} = (\overrightarrow{OA} - \overrightarrow{OM}) \bullet (\overrightarrow{OB} - \overrightarrow{OM}) = \left(\begin{array}{cc} 1 & -x \\ 7 & -y \end{array}\right) \bullet \left(\begin{array}{cc} 8 & -x \\ 3 & -y \end{array}\right) = 0\)
\(\Leftrightarrow (1-x)~(8-x) + (7-y)~(3-y) = 0\)
\(\Leftrightarrow 8-9x + x^{2} + 21 - 10y + y^{2} = 0\)
\(\Leftrightarrow x^{2} + y^{2} - 9x - 10y + 29 = 0\)
ou \(\left(x - \frac{9}{2} \right)^{2} + (y-5)^{2} = \left(\frac{\sqrt{65}}{2} \right)^{2}\) de la forme \((x-x_{0})^{2} + (y - y_{0})^{2} = R^{2}\)
avec \(x_{0} = \frac{x_{A} + x_{B}}{2} = \frac{9}{2}\) et \(y_{0} = \frac{y_{A} + y_{B}}{2} = 5\) les coordonnées du centre du cercle .
Remarque : Le triangle \(ABC\) étant approximativement demi-équilatéral , le sommet \(C\) d'angle \(90^{\circ}\), doit appartenir au cercle \((C_0)\) d'où :
\(x^{2} + y^{2} - 9x - 10y + 29 = \frac{81}{4} + 1 - \frac{81}{2} - 10 + 29 = -\mathrm{0,25} \approx 0\)