Valeurs propres - Vecteurs propres - Diagonalisation d'une matrice carrée
Soit \(\mathcal{E}\) un espace vectoriel sur \(\mathbb{K}\) et \(f\) un endomorphisme de \(\mathcal{E}\).
Définition :
On appelle vecteur propre de \(f\) tout vecteur \(x\), non nul de \(\mathcal{E}\), vérifiant : \(f(x) = \lambda x\).
(Les vecteurs propres sont donc les vecteurs dont la direction est inchangée par l'application \(f\)).
Le scalaire \(l \in \mathbb{K}\) est appelé valeur propre associée au vecteur \(x\).
Calcul des valeurs propres et vecteurs propres
Si \(A = (a _{ij})\) est la matrice de l'application \(f\) dans une base \(B\) de \(\mathcal{E}\) et \(X = \begin{pmatrix} x_{1} \\ x_{2} \\ \ldots \\ x_{n} \end{pmatrix}\) la matrice unicolonne du vecteur propre \(x\) dans \(B\), alors :
\(f(x) = \lambda x \Rightarrow AX = \lambda X \Leftrightarrow \color{red} (A - \lambda I) X = 0\) (\(I\) : matrice unité d'ordre \(n\))
Le système homogène ainsi obtenu :
\(\left\{ \begin{array}{l c l} (a_{11} - \lambda) x_{1} + a_{12}x_{2} + \ldots + a_{1n}x_{n} & = & 0 \\ a_{21}x_{1} + (a_{22} - \lambda) x_{2} + \ldots + a_{2n}x_{n} & = & 0 \\ \ldots \\ a_{n1}x_{1} + a_{n2}x_{2} + \ldots + (a_{nn} - \lambda) x_{n} & = & 0 \end{array} \right.\)
à l'exclusion de la solution triviale \(X = 0\), admettra des solutions si le déterminant de \((A - \lambda I) = 0\).
Les valeurs propres de \(f\) (ou de \(A\)) sont les scalaires \(\lambda\) tels que :
\(\textrm{det}(A - \lambda I) = \left| \begin{matrix} a_{11} - \lambda & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} - \lambda & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & \ldots & \ldots & a_{nn} - \lambda \end{matrix} \right| = 0\)
L'équation de degré \(n\) en \(\lambda\) ainsi obtenu est dite Equation caractéristique.
(voir exemple "Calcul de valeurs propres" ci-dessous)
Un vecteur propre \(x\) de composantes \((x',x",...)\) associé à la valeur propre \(\lambda\) doit vérifier la relation : \(AX = \lambda X \Leftrightarrow (A - \lambda I_{n}) \begin{pmatrix} x' \\ x" \\ \ldots\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \ldots \end{pmatrix}\)
(\(In\) : matrice identité à l'ordre \(n\))
Propriété : Si la matrice \(A\) admet \(p\) valeurs propres, distinctes deux à deux, les \(p\) vecteurs propres associés sont linéairement indépendants et forment une base de l'espace vectoriel \(\mathcal{E}\).
(voir exemple "Calcul de vecteurs propres" ci-dessous)
Exemple : Calcul de valeurs propres
Déterminer les valeurs propres de la matrice \(A = \begin{pmatrix} 5 & -3 \\ 6 & -4 \end{pmatrix}\)
Les valeurs propres de \(A\) sont les scalaires \(l\) vérifiant :
\(\begin{array}{r l} \textrm{det} (A - \lambda I_{2}) = 0 & \Leftrightarrow \left| \begin{matrix} 5-\lambda & -3 \\ 6 & -4 -\lambda \end{matrix} \right| \\ & = -(5 - \lambda)(4 + \lambda) + 18 \\ & =\lambda^{2} - \lambda - 2 \\ & = \color{red} (\lambda + 1)(\lambda -2)= 0\end{array}\)
d'où les valeurs propres : \(\color{red} l_{1} = -1\) et \(\color{red} l_{2} = +2\)
Exemple : Calcul de vecteurs propres
Déterminer les vecteurs propres associés aux valeurs propres de la matrice \(A = \begin{pmatrix} 5 & -3 \\ 6 & -4 \end{pmatrix}\). Les vecteurs propres obtenus forment-ils une base de \(\mathbb{R}^{2}\) ?
En posant \(x_{1}\) et \(x_{2}\) les vecteurs propres associés respectivement à \(l_{1}\) et \(l_{2}\), nous avons :
Pour \(l_{1} = -1\)
\((A + I_{2}) X_{1} = 0 \Leftrightarrow \begin{pmatrix} 6 & -3 \\ 6 & -3 \end{pmatrix}\begin{pmatrix} x'_{1} \\ x"_{1} \end{pmatrix} = 0\)
Le système est équivalent à : \(6x'_{1} - 3x"_{1} = 0\)
Choix d'un vecteur propre : \(x_{1} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)
Pour \(l_{2} = +2\)
\((A - 2I_{2}) X_{2} = 0 \Leftrightarrow \begin{pmatrix} 3 & -3 \\ 6 & -6 \end{pmatrix}\begin{pmatrix} x'_{2} \\ x"_{2} \end{pmatrix} = 0\)
Le système est équivalent à : \(3x'_{2} - 3x"_{2} = 0\)
Choix d'un vecteur propre : \(x_{2} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}\)
Comme le déterminant \(\left| \begin{matrix} 1 & 1 \\ 2 & 1 \end{matrix} \right| \neq 0\), la famille \((x_{1}, x_{2})\) est une base de \(R^{2}\).
Diagonalisation d'une matrice carrée
L'endomorphisme \(f\) de \(\mathcal{E}\) est représenté par la matrice \(A = (a_{ij})\) dans la base \(B = (e_{1}, e_{2},..., e_{n})\).
Cas des valeurs propres distinctes
Les vecteurs propres \(x_{1}, x_{2},..., x_{n}\) associés aux valeurs propres \(\lambda_{1}, \lambda_{2},..., \lambda_{n}\) forment une base \(B_{x} = (x_{1}, x_{2},..., x_{n})\) de \(\mathcal{E}\).
Dans cette base \(B_{x}\), la matrice \(A'\) est diagonale et souvent notée par :
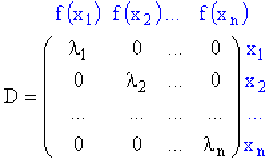
avec \(D = P^{-1}AP\), \(P\) représentant la matrice de passage de la base \(B\) à la base \(B_{x}\).
Exemple : Diagonalisation d'une matrice carré d'ordre 2
Vérifier, à partir des résultats des deux exemples précédents que :
\(D = P^{-1}AP\) avec \(A = \begin{pmatrix} 5 & -3 \\ 6 & -4 \end{pmatrix}\)
La connaissances des valeurs propres \(l_{1} = -1\), \(l_{2} = 2\) et des vecteurs propres associés \(x_{1} = (1,2)\) et \(x_{2} = (1,1)\) conduisent à la matrice de passage \(P\).
\(P = \begin{pmatrix} 1 & 1 \\ 2 & 1 \end{pmatrix} \Rightarrow P^{-1} = - \begin{pmatrix}1 & -1 \\ -2 & 1\end{pmatrix} = \begin{pmatrix} -1 & 1 \\ 2 & -1 \end{pmatrix} (\textrm{det}~P = -1 )\)
et
\(\begin{array}{l c l} \textcolor{red}{D} = P^{-1}AP & = & \begin{pmatrix} -1 & 1 \\ 2 & -1 \end{pmatrix} \begin{pmatrix} 5 & -3 \\ 6 & -4 \end{pmatrix} \begin{pmatrix}1 & 1 \\ 2 & 1\end{pmatrix} \\\\ & = & \begin{pmatrix} 1 & -1 \\ 4 & -2 \end{pmatrix} \begin{pmatrix}1 & 1 \\ 2 & 1\end{pmatrix} \\ \\& = & \color{red} \begin{pmatrix} -1 & 0 \\0 & 2 \end{pmatrix} \end{array}\)
La matrice diagonale est donc formée des valeurs propres .
La diagonalisation d'une matrice est utilisée dans la recherche de puissance de matrices à un ordre \(n \in \mathbb{N}^{*}\).
En effet, de \(D = P^{-1}AP\) en prémultipliant par \(P\) et en postmultipliant par \(P^{-1}\), nous avons : \(PDP^{-1} = PP^{-1}APP^{-1} = A \Rightarrow A = PDP^{-1}\).
L'élévation à une puissance \(n \in \mathbb{N}^{*}\) de la matrice \(A\) conduit à :
\(\color{red} A^{n} \color{black} = \underset{n \textrm{fois}}{\underbrace{\Big( PDP^{-1}\Big) \Big( PDP^{-1}\Big) \ldots \Big( PDP^{-1}\Big)}} = \color{red} PD^{n}P^{-1}\)
avec \(D^{n} = \begin{pmatrix} \lambda_{1}^{n} & 0 & \ldots & 0 \\ 0 & \lambda_{2}^{n} & \ldots & 0 \\ \ldots & \ldots &\ldots & \ldots \\ 0 & 0 &\ldots & \lambda_{n}^{n} \end{pmatrix}\)
Exemple : Diagonalisation d'une matrice carré d'ordre 3
Diagonalisation de la matrice \(A= \begin{pmatrix} 0 & -1 & 0 \\ -1 & 0 & 0 \\ 1& 1& 1\end{pmatrix}\)
Calculons le déterminant de \((A - l~I_{3})\)
\(\begin{array}{l l l}\textrm{det}(A - \lambda I_{3}) & = \left| \begin{matrix} -\lambda & -1 & 0 \\ -1 & -\lambda & 0 \\ 1 & 1 & 1-\lambda \end{matrix} \right| & = -\lambda \left| \begin{matrix} -\lambda & 0 \\ 1 & 1-\lambda \end{matrix}\right| + 1 \left| \begin{matrix} -1 & 0 \\ 1 & 1-\lambda \end{matrix} \right| \\ & & = -\lambda \Big[ -\lambda ( 1 -\lambda ) + (-1)(1 -\lambda) \Big] \\ & & =( 1 -\lambda) \Big[ \lambda^{2} -1 \Big] \\ & & = - ( \lambda - 1)^{2} (\lambda +1) \end{array}\)
Équation caractéristique : \(\textrm{det}(A - l~I_{3}) = 0\) a pour racines les valeurs propres :\(\color{red}l_{1} = l_{2} = 1 (\textrm{double})\) et \(\color{red}l_{3} = -1\).
Recherche des vecteurs propres associés aux valeurs propres.
Pour \(l_{1} = +1\)
\(\begin{pmatrix} -1 & -1 & 0 \\ -1 & -1 & 0 \\ 1 & 1 & 0 \end{pmatrix} \begin{pmatrix} x'_{1} \\ x"_{1} \\ x'''_{1} \end{pmatrix} = 0\)
Les solutions du système sont : \(x'_{1} + x''_{1} = 0\) et \(x'''_{1}\) quelconque
Equation d'un plan vectoriel engendré, par exemple, par les vecteurs linéairement indépendants \(x_{1} = (-1,1,0)\) et \(x_{2} = (0,0,1)\).
Pour \(l_{3} = -1\)
\(\begin{pmatrix} -1 & -1 & 0 \\ -1 & -1 & 0 \\ 1 & 1 & 0 \end{pmatrix} \begin{pmatrix} x'_{3} \\ x"_{3} \\ x"'_{3} \end{pmatrix} = 0 \Leftrightarrow \left\{ \begin{array}{l r c} x'_{3} - x"_{3} & = & 0 \\ -x'_{3} + x"_{3} & = & 0 \\x'_{3} + x"_{3} + 2 x'''_{3} & = & 0 \end{array} \right.\)
Les solutions du système sont : \(x'_{3} = x''_{3} = - x'''_{3}\)
Equation d'une droite vectorielle engendrée, par exemple, par le vecteur \(x_{3} = (1, 1, -1)\),
d'où la matrice de passage \(P = \begin{pmatrix} -1 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & -1 \end{pmatrix}\)
La matrice inverse \(P^{-1}\) peut s'obtenir par la matrice des cofacteurs :
\(P^{-1} = \frac{1}{2} \begin{pmatrix} -1 & 1 & 0 \\ 1 & 1 & 2 \\ 1 & 1 & 0 \end{pmatrix}\), avec \(|P| = 2\).
Donc, \(\begin{array}{r c l} \textcolor{red}{D} = P^{-1} AP & = & \frac{1}{2}~\begin{pmatrix}-1 & 1 & 0\\ 1 & 1 & 2 \\ 1 & 1& 0\end{pmatrix} \begin{pmatrix} 0 & -1 & 0 \\ -1 & 0& 0 \\ 1 & 1 & 1\end{pmatrix} \begin{pmatrix} -1 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & -1\end{pmatrix} \\ & = & \frac{1}{2}~\begin{pmatrix}-1 & 1 & 0\\ 1 & 1 & 2 \\ 1 & 1& 0\end{pmatrix}\begin{pmatrix} -1 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & -1\end{pmatrix} \\ & = & \color{red}\quad \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1& 0 \\ 0 & 0 & -1\end{pmatrix} \end{array}\)