Equivalence RC série/parallèle
Partie
Question
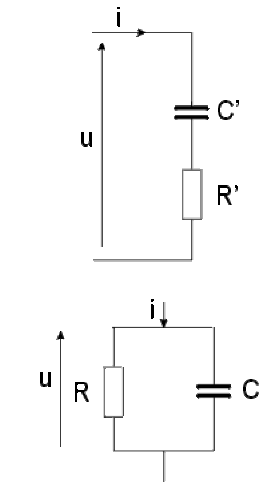
Quelle relation doit-il y avoir entre \(R\), \(R'\), \(C\) et \(C'\) pour que les deux dipôles ci-dessous aient, pour une fréquence donnée, la même impédance ?
Aide simple
Exprimer l'admittance complexe du dipôle \(RC\) ; en déduire son impédance et l'identifier à celle du dipôle \(R'C'\).
Aide détaillée
L'admittance complexe du dipôle équivalent à une association de dipôles en parallèle est égale à la somme des admittances complexes : \(\displaystyle{\underline Y=\sum_n\underline Y_n}\)
L'impédance complexe de dipôles associés en série est égale à la somme des impédances complexes : \(\displaystyle{\underline Z=\sum_n\underline Z_n}\)
Aide méthodologique
Impédances complexes
Solution simple
\(\displaystyle{R'=\frac{R}{1+R^2C^2\omega^2};\;C'=\frac{1+R^2C^2\omega^2}{R^2C^2\omega^2}}\)
Solution détaillée
L'admittance complexe du dipôle équivalent à une association de dipôles en parallèle est égale à la somme des admittances complexes :
\(\displaystyle{\underline Y_{RC}=\underline Y_R+\underline Y_C=\frac{1}{R}+jC\omega=\frac{1+jRC\omega}{R}}\)
\(\displaystyle{\underline Z_{RC}=\frac{1}{\underline Y_{RC}}=\frac{R}{1+jRC\omega}=\frac{R(1-jRC\omega)}{1+jR^2C\omega^2}}\)
L'impédance complexe de dipôles associés en série est égale à la somme de leurs impédances complexes :
\(\displaystyle{\underline Z_{R'C'}=\underline Z_{R'}+\underline Z_{C'}=R'+\frac{1}{jC'\omega}}\)
En identifiant les deux parties réelles des deux expressions, on obtient :\(\displaystyle{R'=\frac{R}{1+R^2C^2\omega^2}}\) et l'identité des parties imaginaires donne :
\(\displaystyle{\frac{1}{C'\omega}=\frac{1+R^2C^2\omega^2}{R^2C^2\omega^2}}\)
qui conduit à :
\(\displaystyle{C'=\frac{1+R^2C^2\omega^2}{R^2C^2\omega^2}}\)
Comme \(\displaystyle{R^2C^2\omega^2> 0,\; R'< R \textrm{ et } C'> C}\). Un montage dans lequel un condensateur \(C\) aurait une résistance de fuite \(R\) peut donc, pour une fréquence donnée, être remplacé par un montage série \(R'C'\) dans lequel la valeur de \(C'\) est d'autant plus proche de celle de \(C\) et la résistance en série avec le condensateur d'autant plus petite que la fréquence est élevée.