Diviseur de tension
Partie
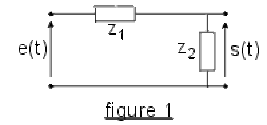
Soit un diviseur de tension (fig 1) formé de deux dipôles d'impédances complexes \(\displaystyle{\underline Z_1\textrm{ et }\underline Z_2}\). On applique à l'entrée du diviseur une tension sinusoïdale : \(\displaystyle{\underline e(t)=E\cos\omega t \quad (\underline e(t)=E.\textrm{e}^{j\omega t})}\) et on exprime la tension de sortie à vide sous la forme : \(\displaystyle{s(t) = S.\cos(\omega t +\varphi)\quad(\underline s(t)=S.\textrm{e}^{j\omega t}.\textrm{e}^{j\varphi})}\) . On pose : \(\displaystyle{g=\frac{S}{E}} ;\)
Question
Exprimer \(g\) et\(\varphi\) en fonction des éléments du montage dans le cas suivant :
cas 1: (fig 2) diviseur \(RC\).
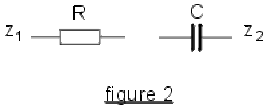
Aide simple
Utiliser les impédances complexes.
Aide détaillée
Deux dipôles en série sont traversés par le même courant
Aide méthodologique
Loi d'Ohm en régime sinusoïdal
Solution simple
Cas général : \(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 1 \(\qquad\) \(\displaystyle{g=\frac{1}{\sqrt{1+(RC\omega)^2}};\;\varphi=-\textrm{Arctg}({RC\omega})}\)
Solution détaillée
Cas général (figure 1) :
La tension \(s(t)\) étant mesurée à vide, les impédances \(\underline Z_1\) et \(\underline Z_2\) sont parcourues par le même courant d'intensité \(i(t)\) ;
d'où les expressions complexes de \(e(t)\) et \(s(t)\) :
\(\displaystyle{\underline e(t)=(\underline Z_1+\underline Z_2).\underline i(t)}\)
\(\displaystyle{\underline s(t)=\underline Z_2.\underline i(t)}\)
et celle du gain complexe :
\(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 1 (figure 2):
\(\displaystyle{\underline Z_1 = R ; ~\underline Z_2=\frac{1}{jC\omega}}\) en reportant ces valeurs dans l'expression du gain complexe, on obtient :
\(\displaystyle{\begin{array}{lll}g.\textrm{e}^{j\varphi} & = & \frac{\underline Z_2}{\underline Z_1+\underline Z_2}=\frac{\frac{1}{jC\omega}}{R+\frac{1}{jC\omega}}\\ & = & \frac{1}{1+{jRC\omega}}\end{array}}\)
dont le module et l'argument sont : \(\displaystyle{g=\frac{1}{\sqrt{1+{(RC\omega)^2}}}} ;\)
\(\displaystyle{\varphi=-\textrm{Arctg}({RC\omega})}\) Valeurs limites :
\(\displaystyle{\omega\to0\Rightarrow g\to1,\varphi\to 0;\;\omega\to\infty\Rightarrow g\to 0,\varphi\to- \frac{\pi}{2}}\)
Ce montage, dont le gain diminue quand la fréquence s'abaisse, est connu sous le nom de filtre \(RC\) passe-bas.
Question
Exprimer \(g\) et\(\varphi\) en fonction des éléments du montage dans le cas suivant :
cas 2: (fig 3) diviseur \(CR\).
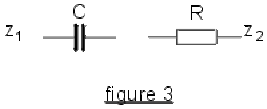
Aide simple
Utiliser les impédances complexes.
Aide détaillée
Deux dipôles en série sont traversés par le même courant
Aide méthodologique
Loi d'Ohm en régime sinusoïdal
Solution simple
Cas général : \(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 2 \(\qquad\) \(\displaystyle{g=\frac{1}{\sqrt{1+\frac{1}{(RC\omega)^2}}};\;\varphi=\textrm{Arctg}\Big(\frac{1}{RC\omega}\Big)}\)
Solution détaillée
Cas général (figure 1) :
La tension \(s(t)\) étant mesurée à vide, les impédances \(\underline Z_1\) et \(\underline Z_2\) sont parcourues par le même courant d'intensité \(i(t)\) ;
d'où les expressions complexes de \(e(t)\) et \(s(t)\) :
\(\displaystyle{\underline e(t)=(\underline Z_1+\underline Z_2).\underline i(t)}\)
\(\displaystyle{\underline s(t)=\underline Z_2.\underline i(t)}\)
et celle du gain complexe :
\(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 2 (figure 3):
\(\displaystyle{\underline Z_1=\frac{1}{jC\omega} ;~\underline Z_2 = R}\) en reportant ces valeurs dans l'expression du gain complexe, on obtient :
\(\displaystyle{\begin{array}{lll}g.\textrm{e}^{j\varphi} & = & \frac{\underline Z_2}{\underline Z_1+\underline Z_2}=\frac{R}{R+\frac{1}{jC\omega}}\\ & = & \frac{1}{1+\frac{1}{jRC\omega}}\end{array}}\)
dont le module et l'argument sont : \(\displaystyle{g=\frac{1}{\sqrt{1+\frac{1}{(RC\omega)^2}}}}\)
\(\displaystyle{\varphi=-\textrm{Arctg}\Big(\frac{1}{RC\omega}\Big)}\) Valeurs limites :
\(\displaystyle{\omega\to0\Rightarrow g\to0,\varphi\to\frac{\pi}{2};\;\omega\to\infty\Rightarrow g\to1,\varphi\to0}\)
Ce montage, dont le gain diminue quand la fréquence s'abaisse, est connu sous le nom de filtre \(RC\) passe-haut.
Question
Exprimer \(g\) et\(\varphi\) en fonction des éléments du montage dans le cas suivant :
cas 3: (fig 4) diviseur \(RL\).
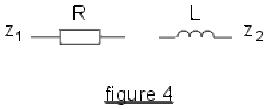
Aide simple
Utiliser les impédances complexes.
Aide détaillée
Deux dipôles en série sont traversés par le même courant
Aide méthodologique
Loi d'Ohm en régime sinusoïdal
Solution simple
Cas général : \(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 3 \(\qquad\) \(\displaystyle{g=\frac{1}{\sqrt{1+\frac{R^2}{(L\omega)^2}}}};\;\varphi=\textrm{Arctg}\Big(\frac{R}{L\omega}\Big)\)
Solution détaillée
Cas général (figure 1) :
La tension \(s(t)\) étant mesurée à vide, les impédances \(\underline Z_1\) et \(\underline Z_2\) sont parcourues par le même courant d'intensité \(i(t)\) ;
d'où les expressions complexes de \(e(t)\) et \(s(t)\) :
\(\displaystyle{\underline e(t)=(\underline Z_1+\underline Z_2).\underline i(t)}\)
\(\displaystyle{\underline s(t)=\underline Z_2.\underline i(t)}\)
et celle du gain complexe :
\(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 3 (figure 4) :
\(\displaystyle{\underline Z_1 = R;\; \underline Z_2 = jL\omega}\) ; en reportant ces valeurs dans l'expression du gain complexe, on obtient :
\(\displaystyle{\begin{array}{lll}g.\textrm{e}^{j\varphi} & = & \frac{\underline Z_2}{\underline Z_1+\underline Z_2}=\frac{jL\omega}{R+jL\omega}\\ & = & \frac{1}{1+\frac{R}{jL\omega}}\end{array}}\)
dont le module et l'argument sont : \(\displaystyle{g=\frac{1}{\sqrt{1+\frac{R^2}{(L\omega)^2}}}}\)
\(\displaystyle{\varphi=-\textrm{Arctg}\Big(\frac{L\omega}{R}\Big)}\) Valeurs limites :
\(\displaystyle{\omega\to0\Rightarrow g\to0,\;\varphi\to\frac{\pi}{2};\;\omega\to\infty\Rightarrow g\to1,\;\varphi\to0}\),
Ce montage, dont le gain diminue quand la fréquence s'abaisse, est connu sous le nom de filtre \(RL\) passe-haut.
Question
Exprimer \(g\) et\(\varphi\) en fonction des éléments du montage dans le cas suivant :
cas 4: (fig 5) diviseur \(LR\).
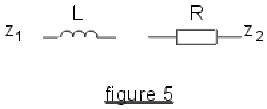
Aide simple
Utiliser les impédances complexes.
Aide détaillée
Deux dipôles en série sont traversés par le même courant
Aide méthodologique
Loi d'Ohm en régime sinusoïdal
Solution simple
Cas général : \(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 4 \(\qquad\) \(\displaystyle{g=\frac{1}{\sqrt{1+\frac{(L\omega)^2}{R^2}}};\;\varphi=-\textrm{Arctg}\Big(\frac{L\omega}{R}\Big)}\)
on pose \(\displaystyle{R=\frac{R_1R_2}{R_1+R_2},\textrm{ et }C = C_1 + C_2}\)
Solution détaillée
Cas général (figure 1) :
La tension \(s(t)\) étant mesurée à vide, les impédances \(\underline Z_1\) et \(\underline Z_2\) sont parcourues par le même courant d'intensité \(i(t)\) ;
d'où les expressions complexes de \(e(t)\) et \(s(t)\) :
\(\displaystyle{\underline e(t)=(\underline Z_1+\underline Z_2).\underline i(t)}\)
\(\displaystyle{\underline s(t)=\underline Z_2.\underline i(t)}\)
et celle du gain complexe :
\(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 4 (figure 5) :
\(\displaystyle{\underline Z_1=jL\omega ;\underline Z_2=R}\) en reportant ces valeurs dans l'expression du gain complexe, on obtient :
\(\displaystyle{\begin{array}{lll}g.\textrm{e}^{j\varphi} & = & \frac{\underline Z_2}{\underline Z_1+\underline Z_2}=\frac{R}{R+jL\omega}\\ & = & \frac{1}{1+\frac{jL\omega}{R}}\end{array}}\)
dont le module et l'argument sont :
\(\displaystyle{g=\frac{1}{\sqrt{1+\frac{(L\omega)^2}{R^2}}}}\);
\(\displaystyle{\varphi=-\textrm{Arctg}\Big(\frac{L\omega}{R}\Big)}\)
Valeurs limites : \(\displaystyle{\omega\to0\Rightarrow g\to1,\;\varphi\to0;\;\omega\to\infty\Rightarrow g\to0,\;\varphi\to-\frac{\pi}{2}}\)
Ce montage, dont le gain diminue quand la frequence s'abaisse est connu sous le nom de filtre \(RL\) passe-bas.
Question
Exprimer \(g\) et\(\varphi\) en fonction des éléments du montage dans le cas suivant :
Pour ce dernier montage, montrer qu'on peut avoir \(\varphi = 0\).
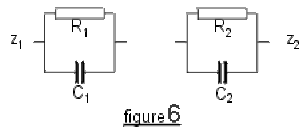
cas 5: (fig 6) diviseur \(RC-RC\)
Aide simple
Utiliser les impédances complexes.
Aide détaillée
Deux dipôles en série sont traversés par le même courant
Aide méthodologique
Loi d'Ohm en régime sinusoïdal
Solution simple
Cas général : \(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 5 \(\qquad\) \(\displaystyle{g=\frac{R}{R_1}=\sqrt{\frac{1+(R_1C_1\omega)^2}{1+(RC\omega)^2}}};\;\varphi=\textrm{Arctg}(R_1C_1\omega-RC\omega)\)
si \(R_1C_1 = R_2C_2\textrm{ alors }g=\frac{R_2}{R_1+R_2}\)
Solution détaillée
Cas général (figure 1) :
La tension \(s(t)\) étant mesurée à vide, les impédances \(\underline Z_1\) et \(\underline Z_2\) sont parcourues par le même courant d'intensité \(i(t)\) ;
d'où les expressions complexes de \(e(t)\) et \(s(t)\) :
\(\displaystyle{\underline e(t)=(\underline Z_1+\underline Z_2).\underline i(t)}\)
\(\displaystyle{\underline s(t)=\underline Z_2.\underline i(t)}\)
et celle du gain complexe :
\(\displaystyle{g.\textrm{e}^{j\varphi}=\frac{\underline Z_2}{\underline Z_1+\underline Z_2}}\)
Cas 5 (figure 6) :
On pose
\(\displaystyle{R=\frac{R_1R_2}{R_1+R_2},\textrm{ et }C=C_1+C_2}\);
\(\displaystyle{\underline Z_1=\frac{R_1}{1+jR_1C_1\omega}}\);
\(\displaystyle{\underline Z_2=\frac{R_2}{1+jR_2C_2\omega}}\)
en reportant ces valeurs dans l'expression du gain complexe, on obtient :
\(\displaystyle{\begin{array}{lll}g.\textrm{e}^{j\varphi} & = & \frac{\underline Z_2}{\underline Z_1+\underline Z_2}=\frac{\frac{R_2}{1+jR_2C_2\omega}}{\frac{R_1}{1+jR_1C_1\omega}+\frac{R_2}{1+jR_2C_2\omega}}\\ & = & \frac{R_2+jR_1R_2C_1\omega}{R_1+R_2+jR_1R_2(C_1+C_2)\omega}\\ & = & \frac{R}{R_1}\frac{1+jR_1C_1\omega}{1+jRC\omega}\end{array}}\)
dont le module et l'argument sont :
\(\displaystyle{g=\frac{R}{R_1}\sqrt{\frac{1+(R_1C_1\omega)^2}{1+(RC\omega)^2}}}\);
\(\displaystyle{\varphi=\textrm{Arctg}(R_1C_1\omega-RC\omega)}\) on peut avoir \(\displaystyle{\varphi=0}\) si \(R_1C_1=R_2C_2=RC\);
alors
\(\displaystyle{g=\frac{R_2}{R_1+R_2}}\)
Le montage ainsi réalisé permet d'obtenir une tension \(s(t)\) en phase avec \(e(t)\) :
c'est un diviseur de tension sans déphasage. On l'utilise, sous le nom de "sonde d'oscilloscope", pour pouvoir mesurer à l'oscilloscope des tensions supérieures au calibre le plus élevé \((g = 1/10 \textrm{ ou }1/100).\)