Introduction à l'étude des systèmes oscillants

Lorsqu'un système physique évolue suivant une loi périodique, celle-ci est généralement de forme quelconque, le système n'est donc pas décrit par un oscillateur harmonique. Cependant :

• d'une part, à condition de ne considérer que des petites variations de \(q(t)\) (approximation des petites oscillations), on constate que certains systèmes se comportent comme des oscillateurs harmoniques.

• d'autre part, on montre mathématiquement que toute oscillation périodique se décompose en une somme d'oscillations harmoniques, de pulsations multiples d'une pulsation donnée appelée pulsation fondamentale (décomposition de Fourrier). L'oscillateur est dit anharmonique.

En effet \(q(t)\) :

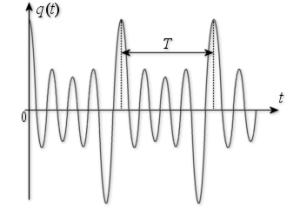
• est une fonction périodique du temps,

• elle est de forme quelconque,

• elle se décompose en une somme de quatre fonctions harmoniques, la première de pulsation \(\omega_0\), les trois autres de pulsations multiples de celle-ci, soit :

  \(q(t) = 2 \sin (0,8~t) + 3 \sin (1,6 ~ t) + 4 \sin (2,4 ~ t) + 5 \sin (3,2 ~ t)\) (unité \(\mathrm{SI}\))

  avec \(\omega_0 = 0,8 ; ~\omega_1 = 2 \omega_0 = 1,6 ; ~\omega_2 = 3 \omega_0 = 2,4 ; ~\omega_3 = 4 \omega_0 = 3,2 ~~(\mathrm{rad.s}^{-1})\)

De nombreux systèmes physiques évoluant suivant des lois périodiques, l'étude du modèle de l'oscillateur harmonique présente un grand intérêt.