Oscillations verticales d'une masse
Durée : 15 mn
Note maximale : 14
Question
On considère un ressort vertical de longueur à vide\(l_{0}\), de masse négligeable et d'élasticité parfaite. Son extrémité supérieure\(O_{1}\)est fixe. On suspend à son extrémité libre une bille de masse\(m = 200g\), assimilée à un point matériel. Le ressort s'allonge alors de la longueur\(l = 5\)cm par rapport à sa longueur à vide jusqu'à atteindre une position d'équilibre. On note\(O\)la position d'équilibre de la masse\(m\), repérée sur l'axe vertical ascendant\((O_{1} ,\vec{e}_{z})\) .
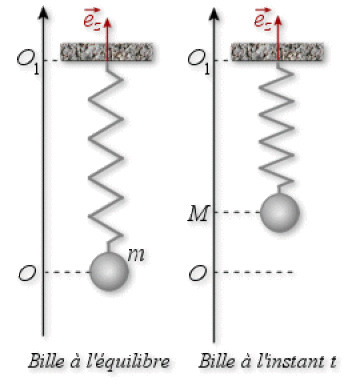
Faire le bilan des forces appliquées à la masse\(m\)à l'équilibre. (1 pt)
Calculer la raideur\(k\)du ressort. (1 pt)
A l'instant\(t=0,\)on communique à la masse la vitesse\(\vec{v}(t=0)=v_{0}.\vec{e}_{z}\)(avec\(v_{0}>0).\) Elle remonte alors de 2 cm avant de redescendre.
Faire le bilan des forces appliquées à la masse et écrire la relation fondamentale de la dynamique. (2 pts)
Après projection sur l'axe\((O_{1} ,\vec{e}_{z})\), en déduire l'équation du mouvement. (2 pts)
Donner la solution de l'équation du mouvement et déterminer l'amplitude maximale des oscillations en fonction de\(v_{0}\), la pulsation et la phase à l'origine. (3 pts)
Calculer les valeurs de\(v_{0}\), de la pulsation, de la période propre et de la fréquence propre des oscillations. (2 pts)
Déterminer à\(t =\frac{T_{0}}{16}\)(\(T_{0}\)étant la période propre du mouvement) la position, la vitesse et l'accélération de la bille. (3 pts)
Solution
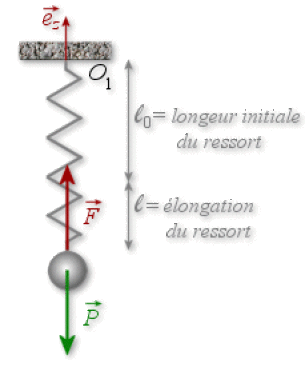
(1 pt) Les forces appliquées à la bille lorsque celle-ci est en équilibre sont :
la force élastique :
\(\displaystyle {\begin{array}{ll} \vec{F_{e}} &=-k\Delta l_{e}\vec{e_{z}} = -k(l_{e} - l_{0})\vec{e_{z}}\\&= kl \vec{e_{z}} (\textrm{avec} l>0) \end{array}}\)
où\(l\)est l'élongation du ressort,
le poids \(\vec{P} = m\vec{g} = -mg.\vec{e_{z}}\).
(1 pt) Pour déterminer la valeur de la raideur du ressort, on écrit la relation fondamentale de la dynamique à l'équilibre :\(\sum\overrightarrow{forces} = \vec{0}\)et après projection sur l'axe\((O_{1},\vec{e}_{z})\) , on obtient la relation :\(\qquad\) \(kl -mg = 0 \Leftrightarrow k = \frac{mg}{l}\)
A.N. :\(k = \frac{\mathrm{0,2}\times\mathrm{9,81}}{\mathrm{0,05}} = \mathrm{39,24}\textrm{N.m}\)
(2 pts) En régime dynamique, les forces appliquées à la bille sont :
la force élastique :
\(\begin{array}{ll} \vec{F_{e}} &=-k\Delta l(t)\vec{e_{z}} = -k(l(t) - l_{0})\vec{e_{z}}\\&= -k(l_{e} + z(t)-l_{0}) \vec{e_{z}} \\&=(-k z(t)+kl). \vec{e_{z}} = k(l-z(t)).\vec{e_{z}}\end{array}\)
où\(l-z(t)\)représente l'allongement instantané du ressort en fonction de la position\(z(t) = \overline{OM}(t)\)de la bille par rapport à la position d'équilibre,
le poids : \(\vec{P} = m\vec{g} = -mg.\vec{e}_{z}\).
La relation fondamentale de la dynamique s'écrit :
\(\sum{\overrightarrow{forces} = m\vec{\gamma}}\)où\(\gamma\)est l'accélération
\(\Leftrightarrow \vec{P} + \vec{F} = m\vec{\gamma}\)
(2 pts) Après projection sur l'axe\((O_{1},\vec{e}_{z})\), on obtient la relation :
\(k(l-z)-mg = m\frac{d^{2}z}{dt^{2}}\Leftrightarrow m\frac{d^{2}z}{dt^{2}} + kz + (mg - kl) = 0\)
Or, d'après la question 2,\(kl-mg = 0\). Il s'ensuit :
\(\frac{d^{2}z}{dt^{2}} + \omega^{2}_{0}z = 0\)avec\(\omega_{0}^{2} = \frac{k}{m}\)
(3 pts) La solution de l'équation précédente est de la forme :
\(z(t) = z_{m}\cos(\omega_{0}t + \varphi)\)où\(z_{m}\)représente l'amplitude des oscillations,\(\omega_{0}\)la pulsation et\(\varphi\)la phase à l'origine.
D'après les conditions initiales, on sait qu'à\(t = 0\), on a :
\(\displaystyle{ \left\{\begin{array}{l l}z(t = 0) = 0\\v(t = 0) = v_{0}\end{array}\right.}\)
Or on a également :
\(\displaystyle{ \left\{\begin{array}{l l}z(t = 0) = z_{m}\cos(\varphi)\\v(t = 0) = -z_{m}\omega_{0}\sin(\varphi)\end{array}\right.}\displaystyle{ \Leftrightarrow\left\{\begin{array}{l l}\cos(\varphi) = 0\\-z_{m}\omega_{0}\sin(\varphi) = v_{0}>0\end{array}\right.}\displaystyle{ \Leftrightarrow\left\{\begin{array}{l l}\varphi = \pm\frac{\pi}{2}\\\varphi <0\end{array}\right.}\displaystyle{\Leftrightarrow \left\{\begin{array}{l l}\varphi = -\frac{\pi}{2}\\z_{m} = \frac{v_{0}}{\omega_{0}}\end{array}\right.}\)
et\(z_{m}^{2} = \frac{v_{0}^{2}}{\omega_{0}^{2}}\)
D'où le résultat :\(\qquad\) \(z(t) = \frac{v_{0}}{\omega_{0}}\cos(\omega_{0}t - \frac{\pi}{2}) =\frac{v_{0}}{\omega_{0}}\sin(\omega_{0}t)\)
(2 pts) D'après le résultat précédent, on sait que\(\frac{v_{0}}{\omega_{0}}\)représente l'amplitude des oscillations. D'après les conditions initiales, on peut en déduire que\(\frac{v_{0}}{\omega_{0}} = 2\textrm{cm}\).
On sait également que :\(\qquad\) \(\omega_{0} =\sqrt{\frac{k}{m}},f_{0} = \frac{2\pi}{\omega_{0}}\)et\(T_{0} = \frac{1}{f_{0}} = \frac{\omega_{0}}{2\pi}\)
A.N. :
\(\omega_{0} = 14~\textrm{rad.s}^{-1}\)
\(f_{0} = \mathrm{2,23}~\textrm{Hz}\)
\(T_{0} = \mathrm{0,449}~\textrm{s}\)
\(v_{0} = \mathrm{0,28}~\textrm{s}^{-1}\)
(3 pts) On reprend la solution de l'équation du mouvement :\(z(t) = \frac{v_{0}}{\omega_{0}}\sin(\omega_{0}t)\)et on remplace t par\(\frac{T_{0}}{16}\)pour connaître la position de la bille. Pour connaître la vitesse de la bille, il faut dériver cette relation une première fois et pour connaître l'accélération, on dérive une deuxième fois l'expression pour finalement trouver :
\(z(t = \frac{T_{0}}{16}) = \mathrm{0,765}.10^{-2}\textrm{m}\)
\(v(t = \frac{T_{0}}{16}) =\mathrm{0,259}\textrm{m.s}^{-1}\)
\(a(t = \frac{T_{0}}{16}) = -\mathrm{1,5}\textrm{m.s}^{-2}\)