Oscillateur harmonique forcé, oscillations forcées

L'excitation est décrite par la force constante \(\overrightarrow{F_{exc}} = F_0 ~\vec e_x\) (où \(F_0\) est une constante).

La réponse de l'oscillateur \(x(t)\) satisfait à l'équation différentielle :

\(x" + 2 \lambda x' + \omega_0^2 x = \frac{F_0}{m}~~\) et \(~~x(t) = x_g(t) + x_p (t)\)

Supposons que les valeurs de \(\lambda = \mu / 2m\) et de \(\omega_0 = \sqrt{k / m}\) de l'oscillateur soient telles que le discriminant réduit \(\Delta'\) soit négatif, dans ce cas la solution générale de l'équation sans second membre s'écrit :

\(x_g (t) = x_m~e^{-\lambda t}~ \cos (\omega_1 t + \varphi)\)

La solution particulière, évidente, s'écrit : \(x_p(t) = \frac{F_0}{m ~\omega_0^2} = \mathrm{ constante}\)

Cet exemple est traité dans la ressource d'exercices sur les oscillations forcées.

L'ensemble des valeurs numériques étant donné, la réponse de l'oscillateur \(x(t)\) ainsi que les fonctions \(x_g(t)\) et \(x_p(t)\) sont représentées dans la figure ci-dessous :

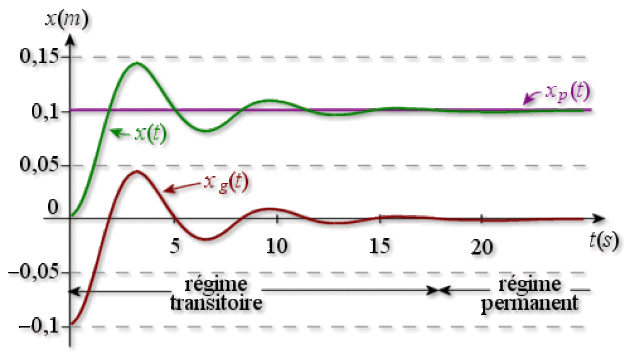
On constate que la réponse en régime permanent est constante. Il n'y a des oscillations que pendant le régime transitoire forcé.