Oscillateur harmonique forcé, oscillations forcées

A tout instant la différence de potentiel aux bornes du générateur est égale à la somme des différences de potentiel aux bornes de \(R\), de \(L\) et de \(C\) : \(u = u_{R} + u_{L} + u_{C} \quad (1)\).

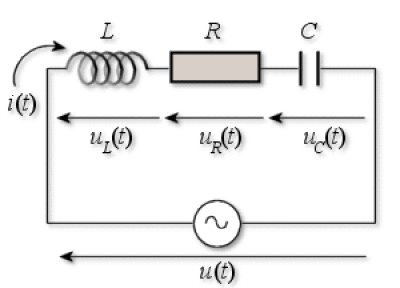
Représentation du circuit à un instant t

Compte tenu du choix de l'intensité et des règles de signes habituelles, il vient :

\(i = C \frac{\textrm{d } u_{C}}{\textrm{d}t}\), \(u_{R} = R~ i = R C \frac{\textrm{d} u_{C}}{\textrm{d} t}\) , \(u_{L} = L \frac{\textrm{d } i}{\textrm{d}t} = LC \frac{\textrm{d}^{2} u_{C}}{\textrm{d} t^{2}}\)

l'équation (1) satisfaite par \(u_{C}(t)\) s'écrit donc en ordonnant les termes :

\(\frac{\textrm{d}^{2} u_{C}}{\textrm{d}t^{2}} + \frac{R}{L} \frac{\textrm{d}u_{C}}{\textrm{d}t} + \frac{1}{LC} u_{C} = \frac{U_{m}}{LC} \cos \Omega~t\)

ou \({u_{C}}'' + 2 \lambda {u_{C}}' + \omega_{0}^{2} u_{C} = \frac{U_{m}}{LC} \cos \Omega~t \qquad (2)\)

équation caractéristique d'un oscillateur harmonique forcé, de coefficient d'amortissement \(\lambda = \frac{R}{2 L}\), de pulsation propre \(\omega_{0} = \frac{1}{\sqrt{LC}}\) et de facteur de qualité \(Q =\frac{ \omega_{0}}{2 \lambda} = \frac{1}{R} \sqrt{\frac{L}{C}}\).

En régime permanent la solution générale \(u_{C}(t)\) de l'équation différentielle  (2), EASM, est très peu différente de la solution particulière \(U_{Cp}(t)\) de cette équation, soit :

\(u_{C}(t) \approx u_{Cp} (t) = U_{Cpm} \cos ( \Omega t + \Phi_{p})\).

On confond habituellement les deux fonctions \(u_{C}(t)\) et \(u_{C p}(t)\) et l'on écrit en posant \(U_{C pm} = A_{m}\) afin de simplifier les notations :

\(u_{C}(t) = A_{m} \cos ( \Omega t + \Phi_{p})\)

Les expressions de l'amplitude \(A_{m}\) et de la phase \(\Phi_{p}\) s'obtiennent à partir de la représentation en amplitude complexe de l'équation (2).

• Ecrivons les correspondances :

  \(\begin{array}{ccccc} \textrm{Grandeur r\'eelle instantan\'ee} & \Leftrightarrow & \textrm{Grandeur complexe instantan\'ee} & \Leftrightarrow & \textrm{Amplitude complexe} \\\\ u_{C}(t) = A_{m}~ \cos (\Omega ~t + \Phi_{p}) & \Leftrightarrow & \underline {u_{C}(t)} = A_{m}~ e^{j~(\Omega ~ t + \Phi_p)} & \Leftrightarrow & \underline {A_{m}} = A_{m}~e^{j \Phi_p} \\\\ {u_{C}}' & \Leftrightarrow & j ~\Omega ~\underline {u_{C}(t)} & \Leftrightarrow & j ~\Omega~ \underline{A_{m}} \\\\ {u_{C}}'' & \Leftrightarrow & - \Omega^{2}~\underline{u_{C}(t)} & \Leftrightarrow & -\Omega^{2}~\underline{A_{m}} \\\\ \frac{U_{m}}{LC}~ \cos \Omega t & \Leftrightarrow & \frac{U_{m}}{LC}~e^{j~\Omega~t} & \Leftrightarrow & \frac{U_{m}}{LC} \end{array}\)

\(\qquad\)

• Déterminons la représentation en amplitude complexe de l'équation (2).

  Pour cela, remplaçons dans cette équation les grandeurs réelles instantanées par les amplitudes complexes correspondantes. En regroupant les termes et en factorisant dans le membre de gauche le terme \(\underline {A_{m}} = A_{m}~e^{j ~\Phi_{p}} \), nous obtenons l'équation complexe :\(\bigg[ (\omega_{0}^{2} - \Omega^{2}) + j(2 \lambda \Omega) \bigg]~A_{m}~e^{j ~\Phi_{p}} = \frac{U_{m}}{LC}\).

  Nous en déduisons l'amplitude complexe \(A_{m}~e^{j ~\Phi_{p}} = \frac{\frac{U_{m}}{LC}}{(\omega_{0}^{2} - \Omega^{2}) + j(2 \lambda \Omega)} \quad (3)\)

• Finalement, l'équation (3), équation entre nombres complexes du type \(\underline{Z_{1}} = \frac{\underline{Z_{2}}}{\underline{Z_{3}}}\) , est équivalente aux deux égalités suivantes :

  • égalité des modules : \(|\underline{Z_{1}} | = \frac{|\underline{Z_{2}}|}{|\underline{Z_{3}}|} \Rightarrow A_{m} = \frac{\frac{U_{m}}{LC}}{\sqrt{( \omega_{0}^{2} - \Omega^{2})^{2} + ( 2 \lambda \Omega)^{2}}} \quad (4)\)

  • égalité des arguments :\(\textrm{arg } \underline{Z_{1}} = \textrm{arg } \underline{Z_{2}} - \textrm{arg } \underline{Z_{3}} \Rightarrow \Phi_{p} = 0 - \textrm{Arc}\tan\frac{2 \lambda \Omega}{\omega_{0}^{2} - \Omega^{2}}\) ou \(\tan ~\Phi_{p} = - \frac{2 \lambda \Omega}{\omega_{0}^{2} - \Omega^{2}}\)

La d.d.p. aux bornes du condensateur, en régime permanent, \(u_{C}(t) = A_{m} ~\cos( \Omega~t + \Phi_{p})\) est déterminée, \(\lambda\) et \(\omega_{0}\) s'exprimant en fonction de \(R, L\) et \(C\).

\(\qquad\)