c. Equations de propagation des composantes
Les deux équations de propagation : \(\Delta \vec E = \varepsilon . \mu . \frac{\partial^2 \vec E}{\partial t^2}\) et \(\Delta \vec B = \varepsilon . \mu . \frac{\partial^2 \vec B}{\partial t^2}\) se résolvent par projection. On obtient respectivement :
\(\Delta E_x = \varepsilon . \mu . \frac{\partial^2 E_x}{\partial t^2}\)
\(\Delta E_y = \varepsilon . \mu . \frac{\partial^2 E_y}{\partial t^2}\)
\(\Delta E_z = \varepsilon . \mu . \frac{\partial^2 E_z}{\partial t^2}\)
\(\Delta B_x = \varepsilon . \mu . \frac{\partial^2 B_x}{\partial t^2}\)
\(\Delta B_y = \varepsilon . \mu . \frac{\partial^2 B_y}{\partial t^2}\)
\(\Delta B_z = \varepsilon . \mu . \frac{\partial^2 B_z}{\partial t^2}\)
Chacune de ces équations admet comme solutions des fonctions de la variable
\(\phi = \vec u . \vec r \pm V . t\)
Démonstration :
Soient \(x\), \(y\), \(z\), les composantes du vecteur position et \(\alpha\), \(\beta\), \(\gamma\) les angles du vecteur unitaire \(\vec u\) avec les axes des coordonnées.
On obtient :
\(\vec u . \vec r = x . \cos(\alpha) + y . \cos(\beta) + z . \cos (\gamma)\)
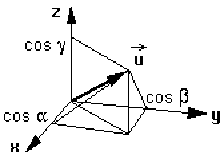
On en tire, par exemple pour l'équation relative à la composante \(E_x\) du champ \(\vec E\) :
\(\frac{\partial E_x}{\partial x} = \frac{\partial E_x}{\partial \phi} . \Big[ \frac{\partial \phi}{\partial x} \Big] = \frac{\mathrm{d} E_x}{\mathrm{d} \phi} . \cos(\alpha)\) d'où l'on déduit la relation entre opérateurs de dérivation : \(\frac{\partial}{\partial x} = \cos(\alpha) . \frac{\mathrm d}{\mathrm d \phi}\)
En appliquant cette relation, on en déduit la nouvelle relation : \(\frac{\partial^2}{\partial x^2} = \cos^2(\alpha) . \frac{\partial^2}{\partial \phi^2}\)
Sachant que le vecteur \(\vec u\) est unitaire, la relation : \(\cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) = 1\) permet alors d'obtenir l'expression du Laplacien de la composante \(E_x\) de \(\vec E\) :
\(\Delta E_x = \frac{\partial^2 E_x}{\partial x^2} + \frac{\partial^2 E_x}{\partial y^2} + \frac{\partial^2 E_x}{\partial z^2} = \frac{\partial^2 E_x}{\partial \phi^2} . [\cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) ] = \frac{\partial^2 E_x}{\partial \phi^2}\)
On montre de même la relation suivante : \(\frac{\partial^2}{\partial t^2} = V^2 . \frac{\mathrm{d}^2}{\mathrm{d} \phi^2}\)
L'équation du Laplacien de la composante sur \(x\) donne alors :
\(\Delta E_x = \frac{\mathrm{d}^2 E_x}{\mathrm{d} \phi^2} = \varepsilon . \mu . \frac{\partial^2 E_x}{\partial t^2} = \varepsilon . \mu . V^2 . \frac{\mathrm{d}^2 E_x}{\mathrm{d} \phi^2}\)
Cette équation est évidemment satisfaite à la condition que :
\(\varepsilon . \mu . V^2 = 1\)
La solution de l'équation de propagation en projection sur \(x\) (concernant la composante sur \(x\) du champ électrique) est donc bien de la forme :
\(E_x(\phi) = E_x (\vec u . \vec r \pm V . t),\)
expression dans laquelle le vecteur unitaire \(\vec u\) est quelconque, et le coefficient \(V\) est parfaitement déterminé :
\(V = \frac{1}{\sqrt{\varepsilon . \mu}}\)
On procèderait de même pour les autres composantes de \(\vec E\) et pour les composantes de \(\vec B\).
On trouverait par exemple pour \(E_y\) une solution de la forme :
\(E_y (\phi) = E_y ( \vec u' . \vec r \pm V.t ),\)
expression où le coefficient \(V\) a la même valeur que précédemment, mais où rien ne permet de savoir si le vecteur unitaire \(\vec u'\) a la même direction que le vecteur unitaire \(\vec u\).
Ce n'est que la signification physique de \(V\) et de ce vecteur unitaire \(\vec u\) qui permettront de répondre à cette question.