Ondes électromagnétiques

Nous nous limitons ici au cas d'une onde électromagnétique plane, polarisée rectilignement. Toutefois ce modèle peut être considéré comme une approximation satisfaisante pour traiter les propriétés d'une onde, à une distance assez grande de la source émettrice.

Soit donc une onde électromagnétique plane polarisée. Sa structure est telle que :

• si \(\vec u\) est le vecteur unitaire dans le sens de la propagation,

• alors \(( \vec E, \vec B, \vec u )\) est un trièdre direct.

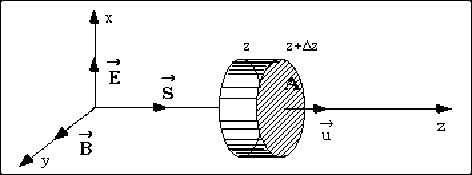
Soit par exemple : \(\vec E\), polarisé selon l'axe \(x\), \(\vec B\) selon l'axe \(y\), et \(z\) la direction de propagation.

La densité d'énergie de l'onde est alors : \(w(z, t) = \frac{\varepsilon E_x^2}{2} + \frac{B_y^2}{2 \mu}\) .

Considérons un domaine de l'espace, dont le volume \(\tau\) est délimité par la surface cylindrique définie par deux surfaces \(A\) orthogonales à la direction \(z\), séparées par une distance \(\Delta z\). On suppose \(\Delta z\) assez petite pour pouvoir considérer que la densité est constante dans ce volume \(\tau\).

L'énergie contenue dans le volume \(\tau\) est donc déterminée par :

\(W(z,t) = \frac{A . \Delta z}{2} \Big(\varepsilon E_x^2 + \frac{B_y^2}{\mu}\Big)\)

D'où, par dérivation : \(\frac{\partial}{\partial t} W(z,t) = A . \Delta z \Big( \varepsilon E_x + \frac{\partial E_x}{\partial t} + \frac{B_y}{\mu} \Big)\)

Les équations de Maxwell : \(\overrightarrow{\mathrm{rot}} ~ \vec E = - \frac{\partial \vec B}{\partial t}\) et \(\overrightarrow{\mathrm{rot}} ~ \vec B = \varepsilon \mu \frac{\partial \vec E}{\partial t} = \frac{1}{\mathrm{c}^2} \frac{\partial \vec E}{\partial t}\)

(pour des milieux homogènes et isotropes, et en dehors des courants) donnent donc ici :

\(\frac{\partial E_x}{\partial t} = - \mathrm{c}^2 \frac{\partial B_y}{\partial z}\) (l'onde étant plane, \(B_y\) n'est fonction que de \(z\) et de \(t\))

\(\frac{\partial B_y}{\partial t} = - \frac{\partial E_x}{\partial z}\) (l'onde étant plane, \(E_x\) n'est fonction que de \(z\) et de \(t\))

Ces relations expriment un couplage entre les composantes des champs \(\vec E\) et \(\vec B\). En les portant dans la relation précédente, on obtient :

\(\frac{\partial}{\partial t} W(z, t) = - A . \Delta z \Big( \varepsilon \mathrm{c}^2 . E_x + \frac{\partial B_y}{\partial z} + \frac{B_y}{\mu} . \frac{\partial E_x}{\partial z} \Big) = - \frac{A . \Delta z}{\mu} \Big( \frac{\partial}{\partial z} (E_x . B_y) \Big)\) ,

expression dans laquelle :

\(\begin{array}{lll} \Delta z \Big( \frac{\partial}{\partial z} (E_x . B_y) \Big) & = & \displaystyle{ \lim_{\Delta z \rightarrow 0}} \Delta z . \bigg( \frac{(E_x . B_y) (z + \Delta z) - (E_x . B_y) (z)}{\Delta z} \bigg) \\  & = & \displaystyle{ \lim_{\Delta z \rightarrow 0}} \big( (E_x . B_y) (z + \Delta z) - (E_x . B_y) (z) \big) \end{array}\)

D'où l'on tire :

Si \(W\) est l'énergie électromagnétique d'un élément de volume \(t\) délimité par une surface fermée constituée d'un tube s'appuyant sur 2 surfaces \(A\) (situées respectivement en \(z\) et en \(z+\Delta z\)) orthogonales à la direction \(z\) de la propagation, alors :

le taux de variation : \(\frac{\partial W}{\partial t}\) (en fonction du temps) de l'énergie \(W\) est égal au produit par \(A\) de la variation de la valeur de la grandeur : \(\frac{E_x . B_y}{\mu}\) , variation exprimée entre les ordonnées \(z\) et \(z + \Delta z\) des surfaces \(A\).