Passages à la limite
On a vu que la période \(T_1\) du fondamental de la série de Fourier d'une fonction périodique est égale à la période \(T\) de la fonction périodique.
la pulsation \(\omega_1\) du fondamental est : \(\omega_1 = \frac{2 \pi}{T_1} = \frac{2 \pi}{T}\)
la pulsation \(\omega_n\) du terme de rang \(n\) dans la série est : \(\omega_n = n.\omega_1\) .
Considérons une suite de fonctions périodiques dont la période tend vers l'infini.
Dans ces conditions :
la pulsation \(\omega_1\) du fondamental de la série tend vers zéro : \(\omega_1 \rightarrow 0\)
l'écart en pulsation \(\delta \omega = \omega_{n+1} - \omega_n\) entre 2 termes de rangs successifs tend lui aussi vers zéro, puisque \(\omega_{n+1} - \omega_n = \omega_1\) .
A la limite lorsque \(\omega_1 \rightarrow 0\), toutes les valeurs de \(\omega\) deviennent possibles : le spectre de la fonction n'est donc plus un spectre discret, mais un spectre continu.
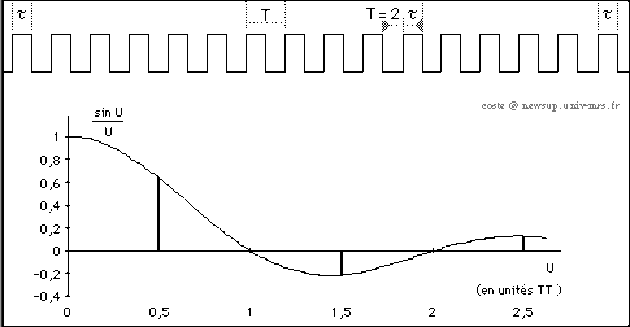
Pour fixer les idées, considérons par exemple la suite des fonctions du temps \(F_s\) carrés, paires, périodiques, dissymétriques, représentées dans la simulation ci-dessous.
Sur une période \(T\) :
\(F_s(t)\) est non-nulle seulement pendant la durée \(t\),
\(F_s(t) = 0\) pendant la durée \(T-t\).
Supposons que la période \(T\) des fonctions \(F_s\) tende vers l'infini de sorte que la durée \(t\) reste constante. Le passage à la limite \(T \rightarrow \infty\) est donc obtenu en faisant tendre le rapport cyclique vers \(0\) : \(\frac{\tau}{T} \rightarrow 0\)
On montre que les coefficients de Fourier d'une fonction carré dissymétrique sont du type :
\(A_n = \frac{4 . \tau}{T} . \frac{\sin U_n}{U_n} ~~~~~~\) avec \(~~ U_n = n \frac{\pi . \tau}{T}\)
Dans ces conditions, lorsque \(\omega_1 \rightarrow 0\) :
les termes du spectre sont de plus en plus resserrés sur l'enveloppe en \(\frac{\sin U}{U}\)
à la limite \(T = \infty\) , il faudrait "attendre un temps infini" avant qu'une autre impulsion carré semblable à la première réapparaisse.
Spectre de cette Fonction Carré Périodique Symétrique Paire
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Analyse de la simulation.
vérifiez que dans le cas d'un rapport cyclique \(k = \frac{1}{2}\) , l'expression du spectre trouvée dans le cas du carré dissymétrique redonne bien les résultats du cas particulier du carré symétrique.
vérifiez que les harmoniques de rang \(n\) multiple de \(\Big( \frac{\tau}{T} \Big)\) sont tous nuls.
notez que l'amplitude des termes de Fourier est définie par :
\(\displaystyle{A_n = \frac{4 . \tau}{T} . \frac{\sin U_n}{U_n} ~~~~~~}\) donc \(~~ A_n \rightarrow 0\) lorsque \(\frac{\tau}{T} \rightarrow 0\)
notez que :
\(\displaystyle{\frac{A_n}{\omega_1} = \frac{4 . \tau}{T} . \frac{\sin U_n}{U_n} . \frac{T}{2 . \pi} = \frac{2 . \tau}{\pi} . \frac{\sin U_n}{U_n} ~ \rightarrow ~ \frac{2 . \tau}{\pi} . \frac{\sin U}{U} ~~}\) quand \(\omega_1 \rightarrow 0\)
Pour cette raison, on est amené à considérer la limite des rapports \(\frac{A_n}{\omega_1}\) qui représentent la densité d'amplitude à la valeur \(\omega = \omega_n\).
(L'appellation de densité d'amplitude se justifie de la même façon que toute autre densité. Par exemple, une charge \(\mathrm{d}q\) divisée par la surface \(\mathrm{d}S\) qui la porte représente la densité \(s\) de charge sur l'élément \(\mathrm{d}S\) considéré).
le Spectre Discret devient un Spectre Continu, représenté par le passage à la limite du rapport \(\frac{A_n}{\omega_1}\) si cette limite existe (quand \(\omega_1 \rightarrow 0\)).
la somme sur les valeurs discrètes de la pulsation (\(\omega_n = n.\omega_1\)) devient alors une intégrale sur la variable continue \(\omega\) (Transformée de Fourier de la Fonction).
Ce passage à la limite permet de comprendre la représentation en fréquences des fonctions non-périodiques à partir de la représentation en fréquences des fonctions périodiques :
Méthode :
Soit une fonction \(F\), non-périodique,
à support borné (nulle à l'infini),
possédant un nombre fini de discontinuités entre \(- \infty\) et \(+ \infty\)
de module carré sommable de \(- \infty\) à \(+ \infty\)
Cette fonction peut être considérée comme une fonction périodique, de "période infinie", i.e. dont les valeurs non-nulles se reproduiraient en ajoutant l'infini à la variable.
Une telle fonction \(F(t)\) sera représentée par le spectre continu \(f(\omega)\) défini par la transformée de Fourier de la fonction \(F\).
Ce passage à la limite est explicité sur le tableau de synthèse en fin de chapitre.
Après avoir défini la transformée de Fourier d'une fonction \(F\) à support borné, on pourra également considérer un autre passage à la limite qui permettra, cette fois-ci, de construire la série de Fourier d'une fonction périodique (§ C2.c).