Exemple : impulsion temporelle en créneau
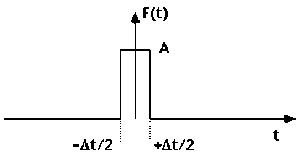
Soit une vibration \(F(t)\) dont l'amplitude est :
constante et égale à \(A\) pendant l'intervalle \(\Delta t\), centré à l'origine,
nulle en dehors de cet intervalle.
Cette vibration est représentée par une fonction \(F\) qui satisfait les conditions suffisantes (support borné, nombre fini de discontinuités, module carré sommable) pour que sa transformée de Fourier existe.
Soit \(f(\omega)\) sa transformée de Fourier, i.e. la densité d'amplitude de \(F(t)\) sur la base des \(\mathrm{e}^{\mathrm{i} . \omega t}\).
Pour calculer \(f(\omega)\), l'amplitude de \(F\) étant nulle en dehors de l'intervalle \(\Big[ - \frac{\Delta t}{2} ~ , + \frac{\Delta t}{2} \Big]\) , il ne reste à calculer que l'intégrale sur cet intervalle, support de la fonction \(F\).
Soit
\(\displaystyle{f(\omega) = \frac{A}{2.\pi} \int_{-\Delta t/2}^{+\Delta t/2} \mathrm{e}^{-\mathrm{i} . \omega t} .\mathrm{d}t = \frac{A}{2 . \pi} ~ . ~ \frac{1}{- \mathrm{i} \omega} \Big( \mathrm{e}^{-\mathrm{i} . \omega \frac{\Delta t}{2}} - \mathrm{e}^{+\mathrm{i} . \omega \frac{\Delta t}{2}}\Big) = \frac{A}{\pi . \omega} \sin \Big( \omega . \frac{\Delta t}{2} \Big)}\)
\(\displaystyle{f(\omega) = \frac{A . \frac{\Delta t}{2}}{ \pi . \omega . \frac{\Delta t}{2}} ~ . ~ \sin\Big(\omega . \frac{\Delta t}{2} \Big) = \frac{A . \Delta t}{2 . \pi} ~ . ~ \frac{ \sin\Big(\omega . \frac{\Delta t}{2} \Big) }{ \omega . \frac{\Delta t}{2} }}\)
\(\displaystyle{f(\omega) = \frac{A . \Delta t}{2 . \pi} . \frac{\sin U}{U} \textrm{ avec } U = \omega . \frac{\Delta t}{2}}\)
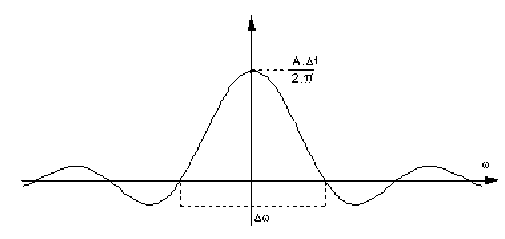
La densité d'amplitude \(f(\omega)\) est donc proportionnelle au produit : \(A . \Delta t\) de la hauteur \(A\) par la largeur \(\Delta t\) du créneau. Ce spectre \(f(\omega)\) est donc aussi celui d'une impulsion dont la durée tendrait vers zéro et dont la hauteur tendrait vers l'infini, de sorte que :
\(A . \Delta t = \mathrm{constante}\).
On pourra montrer en exercice les relations suivantes :
\(\Delta \omega . \Delta t = 4 \pi\)
\(\Delta K . \Delta z = 4 \pi\)
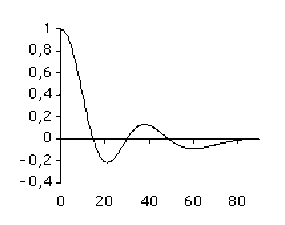
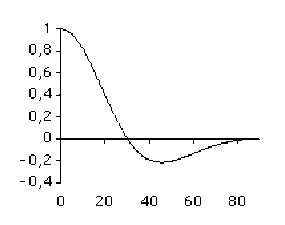
Dans ces expressions, \(\Delta \omega\) et \(\Delta K\) représentent la largeur de la bande spectrale qui contient le maximum central de la densité d'amplitude \(f(\omega)\). Autrement dit, quand la durée \(\Delta t\) du signal diminue, sa largeur spectrale \(\Delta \omega\) augmente.
De la même façon, quand la largeur \(\Delta z\) du support de la fonction diminue, la largeur spectrale \(\Delta K\) augmente.
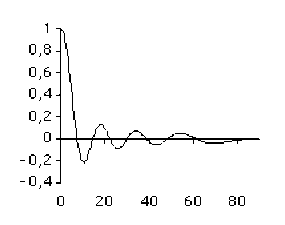
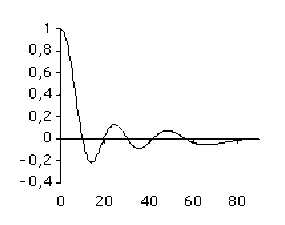
Les 4 schémas ci-dessous (colonne de gauche) montrent cette augmentation de la largeur spectrale lorsque la largeur du support de la fonction diminue.
Ce résultat est à relier à celui qui correspond au spectre de fonctions périodiques carrés dont le rapport cyclique diminuerait.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Passage à la limite : Transformée - Série de Fourier.
Ayant calculé la Transformée de Fourier de cette fonction créneau, il est possible de calculer les spectres d'une suite de fonctions définie à partir de la fonction créneau mais à laquelle on ajouterait successivement de nouveaux créneaux. On peut prévoir que dans cette opération, à force d'ajouter régulièrement de nouveaux créneaux on finirait par tendre vers le spectre d'une fonction carré périodique. C'est ce que montre le calcul et c'est également ce qu'illustre la simulation ci-dessous.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Revoyez, éventuellement, le passage à limite qui a été défini (§ C.2.a) dans le sens Série-Transformée de Fourier...
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.