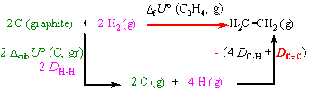Question 2
Énoncé
Déterminer l'énergie de dissociation (DC=C) de la double liaison C=C, en kJ.mol-1, de l'éthylène C2H4.
Données pour 298 K :
Énergie libre molaire standard de formation de l'éthylène gazeux (g) :\( \Delta_f U°\) = 54,8 kJ.mol–1.
Énergie libre molaire standard de sublimation du carbone graphite : \(\Delta_{sub}U°\) = 718,5 kJ.mol–1.
Énergie libre moyenne de dissociation de la liaison C_H : DC-H = 405 kJ.mol–1.
Énergie libre de dissociation de la liaison H-H : DH-H = 432 kJ.mol–1.
Aide simple :
Équation de la réaction de formation de l'éthylène : 2 C (graphite) + 2 H2 (g) \(\rightarrow\) H2C=CH2 (g)
Rappel de cours :
Deux méthodes équivalentes peuvent être utilisées, exploitant le fait que l'énergie interne est une fonction d'état :
Cycle de Hess ;
Combinaison linéaire d'équations de réaction.
Résultat
Correction
Explications
Méthode utilisant un cycle de Hess :
Comme U est une fonction d'état, il vient :
\(\Delta_fU°(C_2H_4, g) =2 \Delta_{sub}U° + 2 D_{H-H} - (4 D_{C-H} + D_{C=C})\)
d'où :
\(D_{C=C} = – \Delta_fU°(C_2H_4, g) + 2 \Delta_{sub}U° + 2 D_{H-H} – 4 D_{C-H} = – 54,8 + (2 \times 718,5) + (2 \times 432) - (4 \times 405)\) = 626,2 kJ.mol–1.
Méthode utilisant la combinaison linéaire des équations de réactions et des énergies mises en jeu :
\(\frac{\begin{array}{c c c c c c} &&2C(graph)&=&2C(g) &2\Delta_{sub}U° \\ &&2 H_2(g)&=& 4 H (g)& 2 D_{H-H} \\ 2C(g)&+&4H(g)&=&H_2C=CH_2(g)& -4D_{C-H} - D_{C=C}\end{array}}{\begin{array}{c c c c c c} 2C(graph)&+&2H_2 (g)&=&H_2C=CH_2(g) & \Delta_fU°(C_2H_4, g)\\ \end{array}}\)