Approche expérimentale des lois de vitesse

La pression totale d'un système gazeux est reliée au nombre de moles de gaz par une relation d'état, dont la forme la plus simple est l'équation des gaz parfaits :

Si la réaction s'accompagne d'une variation du nombre de moles de gaz, en opérant dans une enceinte de volume constant et à température constante, la pression totale variera et il sera facile de relier l'avancement de réaction à la pression totale.

Schéma de principe simplifié de l'appareil :

Considérons la réaction de décomposition de l'hémipentoxyde d'azote :

Soient

• \(P_0\) la pression initiale et \(n_{\textrm A,0}\) la quantité initiale de \(\textrm A\), les quantités initiales de \(\textrm B\) et \(\textrm C\) étant nulles.

• \(P\) la pression totale à l'instant \(t\)

• \(V\) le volume et

• \(T\) la température.

A l'instant \(t = 0\), on peut écrire \(\mathbf{P_0=\frac{n_{\textrm A,0}}{V}.R.T=C_{\textrm A,0}.R.T}\).

Soit \(\xi\) l'avancement de la réaction à l'instant \(t\) . \(\mathbf{\xi=\frac{n_\textrm A-n_{\textrm A,0}}{-2}=\frac{n_\textrm B}{4}=\frac{n_\textrm C}{1}}\)

Les quantités de \(\textrm A\), \(\textrm B\) et \(\textrm C\) à cet instant t sont respectivement :

Le nombre total de moles est donc \(n=n_\textrm A+n_\textrm B+n_\textrm C=n_{\textrm A,0}+3.\xi\).

Que l'on relie à la pression totale par : \(P=n.\frac{R.T}{V}=(n_{\textrm A,0}+3.\xi).\frac{R.T}{V}\).

D'où \(P-P_0=3.\xi.\frac{R.T}{V}\) et finalement \(\xi=\frac{(P-P_0).V}{3.R.T}\).

Puisqu'on opère à volume constant, il est pratique d'utiliser l'avancement volumique \(\frac{\xi}{V}=\frac{(P-P_0)}{3.R.T}\).

Soient \(P_0\) la pression initiale : \(P_0=n_{\textrm A,0}.\frac{R.T}{V}\).

\(P\) la pression à un instant \(t\) d'avancement \(\xi\) : \(P=(n_{\textrm A,0}+3.\xi).\frac{R.T}{V}\).

\(P_\infty\) la pression lorsque la réaction est complète : \(P_\infty=\frac{5}{2}.n_{\textrm A,0}.\frac{R.T}{V}\).

Il vient immédiatement : \(\frac{P-P_0}{P_\infty-P_0}=\frac{2.\xi}{n_{\textrm A,0}}\).

Notons que \(2.\xi\) est la quantité de \(\textrm A\) tranformée à un instant donné.

Posons \(x = 2.\xi\) cette quantité. Le rapport \(\alpha=\frac{x}{n_{\textrm A,0}}\) est appelé fraction transformée de \(\textrm A\).

On obtient : \(\mathbf{\frac{P-P_0}{P_\infty-P_0}=\frac{x}{n_{\textrm A,0}}=\alpha}\).

Cette relation est applicable à toute grandeur physique \(X\) dont la valeur est reliée aux quantités ou concentrations des espèces présentes dans le milieu par une relation linéaire. Nous la noterons donc comme une relation importante pour ces applications pratiques :

Si les réactifs ne sont pas initialement dans des les proportions stoechiométriques, la fraction transformée \(\alpha\) doit être définie pour le réactif minoritaire.

Si une réaction en phase condensée produit un constituant gazeux, il sera facile de suivre l'avancement de la réaction en mesurant le volume de gaz produit en fonction du temps.

Notez que le volume dégagé étant proportionnel à la quantité formée du (ou des) produit(s) gazeux formés, on peut utiliser la relation générale vue ci-dessus en l'appliquant au volume. Le volume initial étant égal à 0 la relation se simplifie en \(\mathbf{\alpha=\frac{V}{V_\infty}}\).

Si le volume molaire des réactifs et des produits sont suffisamment différents, il peut être possible de suivre l'avancement de la réaction en mesurant les variations de volume du système. Pour cela on emploie un dilatomètre constitué d'un vase de réaction soigneusement thermostaté relié à un une tige très fine, on mesure simplement la hauteur de liquide dans cette tige (comme pour un thermomètre).

Notez que, dans ce cas également et sauf cas particulier, le volume total du système est une fonction affine des quantités de chaque constituant, on peut utiliser la relation générale vue ci-dessus en l'appliquant au volume \(\mathbf{\alpha=\frac{V-V_0}{V_\infty-V_0}}\) ou si on mesure la hauteur de liquide dans le tube du dilatomètre \(\mathbf{\alpha=\frac{h-h_0}{h_\infty-h_0}}\).

La masse totale d'un système fermé ne varie pas avec l'avancement des réactions qui peuvent se produire à l'intérieur de ce système, puisque par définition un système fermé est un système qui n' échange pas de matière avec l'extérieur. Lorsqu'une réaction se produit avec un changement de phase par exemple la consommation d'un métal dont les ions passent en solution, la réaction peut parfois être suivie en déterminant la variation de masse d'une partie du système.

Elle repose sur la mesure de l'intensité de la lumière absorbée par une solution ou un gaz placé dans une cellule.

La loi de Beer-Lamber\( \mathbf{\frac{I}{I_0}=\exp^{-\epsilon.C.l}}\) donne le rapport de l'intensité de la lumière transmise \(I\) à l'intensité de la lumière incidente \(I_0\) en fonction du coefficient d'extinction moléculaire \(\epsilon\) de la substance absorbance à la longueur d'onde considérée, de sa concentration \(C\) et de la longueur \(l\) traversée par la lumière.

La spectrophotométrie est surtout employée pour les longueurs d'onde correspondant à la lumière visible (entre 400 nm et 700 nm) et à l'UV (en dessous de 400 nm). La réaction peut avoir lieu directement à l'intérieur de la cellule de mesure. Dans ce cas on utilise des cellules à double enveloppe pour pouvoir contrôler la température dans la cellule en maintenant une circulation d'eau thermostatée dans la double enveloppe. Pour les gaz, on utilise des cellules ayant une plus grande longueur. On peut ainsi suivre en continu la variation de l'intensité de la lumière transmise, pour une longueur d'onde fixe. On fixe généralement cette longueur d'onde au maximum d'absorption d'une des substances participant à la réaction. Avec certains appareils, on peut suivre simultanément plusieurs longueur d'onde. Moyennant certaines précautions, on peut en déduire la variation de concentration de la substance absorbante.

La spectrophotométrie est donc une technique de prédilection car les mesures sont simples et rapides. Cependant, pour étudier des réactions extrêmement rapides, il est difficile, voire impossible de faire des mesures à des instants suffisamment rapprochés pour pouvoir suivre avec précision l'évolution de la réaction. On a alors recours à des méthodes particulières telles que les méthodes à flux continu. Dans ce type de méthode, au lieu de préparer le mélange réactionnel dans un réacteur statique à un instant \(t = 0\) et suivre son évolution, on amène les réactifs en continu pour les mélanger.

La polarimétrie repose sur la mesure du pouvoir rotatoire d'une solution placée dans une cellule.

Si une des substance participant à la réaction est chirale, elle dévie le plan de polarisation selon la loi Biot \(\mathbf{\alpha=[\alpha].C.l}\) relation dans laquelle \(\alpha\) est l'angle de rotation du plan de la lumière polarisée qui traverse la solution. Attention à ne pas le confondre avec a la fraction transformée définie plus haut.\( [\alpha]\) est le pouvoir rotatoire spécifique de la substance optiquement active. \(C\) est sa concentration dans la solution et \(l\) est la longueur de la cellule traversée par la lumière polarisée.

Elle repose sur la mesure de la résistance (ou ce qui revient au même de son inverse, la conductance) du milieu réactionnel.

En solution, il y a variation de la conductance si la réaction entraîne l'apparition ou la disparition d'un ion, ou encore le remplacement d'un ion par un autre. En solution diluée, la conductivité électrique d'une solution est une grandeur additive par rapport aux concentrations des espèces chargées. En négligeant la conductivité du solvant, la conductivité d'un électrolyte est reliée aux concentrations des ions par une relation du type : \(\mathbf{\Lambda=\displaystyle{\sum_i}\lambda_i.C_i}\) relation dans laquelle \(\Lambda\) est la conductivité de la solution. La sommation porte sur tous les ions en solutions.

\(C_i\) est la concentration de l'ion \(i\), \(\lambda_i\) est une grandeur caractéristique de cet ion est appelée conductivité équivalente.

Soient :

• \(\Lambda_0\) la conductivité au temps \(t = 0\)

• \(\Lambda_t\) la conductivité au temps \(t\)

• et \(\Lambda_{0\infty}\) la conductivité lorsque la réaction est complète.

On peut déterminer la fraction transformée \(\alpha\) (rapport entre la quantité transformée et la quantité initiale pour le réactif minoritaire) en appliquant la relation générale et écrire directement \(\mathbf{\alpha=\frac{\Lambda_t-\Lambda_0}{\Lambda_\infty-\Lambda_0}}\).

A partir de \(\alpha\) il est facile de calculer l'avancement de la réaction. En effet nous venons de définir \(\alpha\) par \(\mathbf{\alpha=\frac{x_i}{C_{i,0}}}\) étant le réactif minoritaire et \(C_{i,0}\) sa concentration initiale. Par définition, l'avancement de la réaction s'écrit \(\mathbf{\xi=\frac{x_i}{\nu_i}}\), d'où \(\mathbf{\xi=\frac{\alpha.C_{i,0}}{\nu_i}}\): .

La mesure de la résistance de la solution est simple.

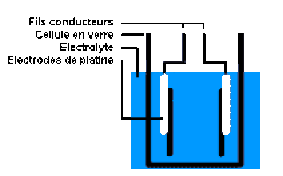
Elle se fait dans une cellule de mesure qui comporte deux plaques métalliques (généralement rectangulaires) permettant d'isoler une petite quantité de solution et d'un appareil de mesure électrique qui donne directement la résistance (ou son inverse).

Note : vous trouverez une description détaillée de cette réaction, de la manipulation et du traitement des données dans la partie Observer, Approche expérimentale, Hydrolyse de l'acétate d'éthyle, étude par conductimétrie.

Elle repose sur la mesure du potentiel d'équilibre d'une électrode, siège d'une réaction électrochimique, placée dans la solution.

Il existe de nombreuses électrodes dont le potentiel est directement relié au logarithme de l'activité (assimilable en solution diluée à la concentration) d'un ion. Nous n'en présenterons ici que les plus importantes.

• Les électrodes dites du premier type sont constituées d'un couple métal / ion métallique et l'électrode à hydrogène, (voir module d'électrochimie), leur potentiel d'équilibre obéit à l'équation de Nenrst : \(\mathbf{E=E°+\frac{R.T}{n.\textrm F}.\ln(\textrm M^{n+})}\) relation dans laquelle \((\textrm{Mn}^+)\) est l'activité (assimilable à la concentration en première approximation) de l'ion \(\textrm{Mn}^+\), \(E_0\) est le potentiel de référence du couple oxydo / réducteur de la réaction qui a lieu sur l'électrode. \(\textrm F\) est la constante de Faraday.

• L'électrode dite "de verre" permet la mesure du \(\textrm{pH}\) donc de l'activité des ions \(\textrm H_3\textrm O^+\) en solution.

  L'électrode de verre, et l'électrode de référence au calomel sont souvent réunies dans une seule sonde appelée électrode combinée.

L'électrode de verre est constituée d'un bulbe de verre, à paroi très mince contenant un électrolyte (\(\textrm{pH = 7,00}\)) dans lequel plonge un fil d'argent recouvert de \(\textrm{AgCl}\).

D'autres électrodes, telles que l'électrode \(\textrm{Ag / AgCl}\), ou des électrodes dites spécifiques permettent aussi de déterminer la concentration d'une espèce présente dans le milieu par une simple mesure de différence de potentiel par rapport à une référence.

En pratique, on mesure la différence de potentiel \(DV\) d'une pile constituée de l'électrode de mesure et d'une électrode de référence dont le potentiel \(E_\textrm{ref}\) est connu.

\(\mathbf{DV = E - E_\textrm{ref}}\). Comme électrode de référence, on utilise souvent l'électrode au calomel saturé.

Le calomel est le nom donné au chlorure mercureux \(\textrm{HgCl}_2\) qui est un sel pratiquement insoluble.

L'électrode au calomel est constituée d'une petite quantité de mercure (jouant le rôle d'électrode) au contact avec le calomel.

Le contact avec la solution est assuré par une solution de \(\textrm{KCl}\) saturé.

La réaction d'oxydo réduction est la suivante :

Son potentiel de référence à 25°C est \(E° = \textrm{0,2445 V}\).