Diagramme de Pourbaix (potentiel-pH) du chlore
Ce diagramme permet de discuter, pour toute valeur de et de potentiel électrochimique, de la stabilité relative des espèces chlorées en solution aqueuse. L'idée est de diviser le plan (E\textrm{,pH}) en zones où une espèce prédomine sur les autres.
Nous considérerons ici seulement les degrés d'oxydation -I, 0 et +I, car :
on s'intéresse surtout aux applications pratiques à la stabilité de l'eau de Javel et de l'eau de chlore,
les D.O. plus élevés sont souvent métastables, ce qui fait que les prédictions thermodynamiques ne sont pas d'une grande utilité concrète.
Voici le diagramme obtenu pour une concentration totale en atomes de chlore c_0=0\textrm,1 \textrm{mol.L}^{-1}
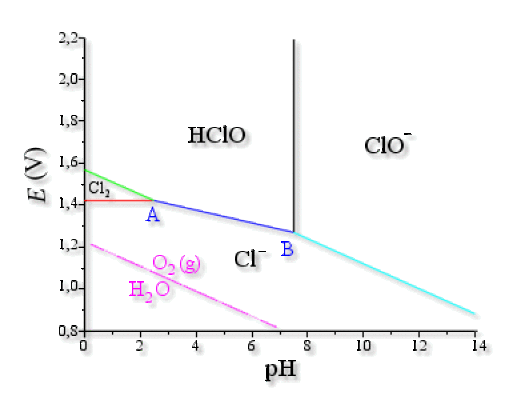
Explication : Construction du diagramme de Pourbaix
Dans ce cours, le dichlore \textrm{Cl}_2 est considéré à l'état gazeux. Il y a un décalage de +0,03 V si on prenait celui-ci à l'état dissous.
On considère les données suivantes :
E°\textrm{(Cl}_2\textrm{/Cl}^-\textrm)=1\textrm,36 \textrm V à \textrm{pH}=0
E°\textrm{(HClO}\textrm{/Cl}_2\textrm)=1\textrm,63 \textrm V à \textrm{pH}=0
\textrm{HClO/Cl}^- : pK_a=7\textrm,5
c_0=0\textrm,1\textrm{ mol.L}^{-1}
On classe les différentes espèces :

Frontière \textrm{HClO/ClO}^-
Le chlore ne change pas de degré d'oxydation (+I), seul le \textrm{pH} intervient.
\textrm{HClO}+\textrm H_2\textrm O\to\textrm H_3\textrm O^++\textrm{ClO}^-
\textrm{pH}=pK_a+\log\frac{[\textrm{ClO}^-]}{[\textrm{HClO}]}
par convention on prend [\textrm{ClO}^-]+[\textrm{HClO}]=c_0 et [\textrm{ClO}^-]=[\textrm{HClO}] \Longrightarrow [\textrm{ClO}^-]=[\textrm{HClO}]=\frac{c_0}{2}
donc \textrm{pH}=pK_a=7\textrm,5

Frontière \textrm{Cl}_2\textrm{/Cl}^-
Seul le degré d'oxydation du chlore change (0\to-I), le \textrm{pH} n'intervient pas.
E\textrm{(Cl}_2\textrm{/Cl}^-\textrm)=E°\textrm{(Cl}_2\textrm{/Cl}^-\textrm)+\frac{0\textrm,06}{1}\log\frac{(p_{\textrm{Cl}_2})^{1/2}}{[\textrm{Cl}^-]}
(application de la loi de Nernst avec \frac{1}{2}.\textrm{Cl}_2+\textrm e^-\to\textrm{Cl}^-)
L'activité du gaz \textrm{Cl}_2 est égale à sa pression et par convention on considère p_{\textrm{Cl}_2}=1\textrm{ bar}.
De plus [\textrm{Cl}^-]=c_0. Donc :
E\textrm{(Cl}_2\textrm{/Cl}^-\textrm)=E°\textrm{(Cl}_2\textrm{/Cl}^-\textrm)+\frac{0\textrm,06}{1}\log\frac{1}{c_0}=1\textrm,36+\frac{0\textrm,06}{1}\log\frac{1}{0\textrm,1}=1\textrm,42 \textrm V

Frontière \textrm{HClO/Cl}_2
Cette frontière fait intervenir à la fois un changement de \textrm{pH} et de degré d'oxydation.
La réaction est :
2.\textrm{HCl}^{+\textrm I}\textrm O+2.\textrm e^-+2.\textrm H^+\to\textrm{Cl}^0_2+2.\textrm H_2\textrm O
L'équation de Nernst nous donne :
E\textrm{(HClO/Cl}_2\textrm)=E°\textrm{(HClO/Cl}_2\textrm)+\frac{0\textrm,06}{2}\log\frac{[\textrm{HClO}]^2[\textrm{H}^+]^2}{p_{\textrm{Cl}_2}}
Avec E°\textrm{(HClO/Cl}_2\textrm)=1\textrm,63 \textrm V , p_{\textrm{Cl}_2}=1 \textrm{bar} et [\textrm{HClO}]=c_0
E\textrm{(HClO/Cl}_2\textrm)=1\textrm,63+\frac{0\textrm,06}{2}\log\frac{[\textrm{HClO}]^2[\textrm{H}^+]}{p_{\textrm{Cl}_2}}
E\textrm{(HClO/Cl}_2\textrm)=1\textrm,63+\frac{0\textrm,06}{2}\log\frac{[\textrm{HClO}]^2}{p_{\textrm{Cl}_2}}+\frac{0\textrm,06}{2}\log[\textrm H^+]^2
E\textrm{(HClO/Cl}_2\textrm)=1\textrm,63+\frac{0\textrm,06}{2}\log\frac{(10^{-1})^2}{1}+0\textrm,06\log[\textrm H^+]=1\textrm,57-0\textrm,06 \textrm{pH}

Frontière \textrm{HClO/Cl}^-
Cette frontière fait intervenir à la fois un changement de \textrm{pH} et de degré d'oxydation.
La réaction est :
\textrm{HCl}^{+\textrm I}\textrm O+2.\textrm e^-+\textrm H^+\to (\textrm{Cl}^-)^{-\textrm I}+\textrm H_2\textrm O
E\textrm{(HClO/Cl}^-\textrm)=E°\textrm{(HClO/Cl}^-\textrm)+\frac{0\textrm,06}{2}\log\frac{[\textrm{HClO}][\textrm{H}^+]}{{[\textrm{Cl}^-]}}
avec par convention [\textrm{Cl}^-]+[\textrm{HClO}]=c_0 et [\textrm{Cl}^-]=[\textrm{HClO}] \Longrightarrow[\textrm{Cl}^-]=[\textrm{HClO}]=\frac{c_0}{2}
E\textrm{(HClO/Cl}^-\textrm)=E°\textrm{(HClO/Cl}^-\textrm)\frac{0\textrm,06}{2}\log[\textrm H^+]=E°\textrm{(HClO/Cl}^-\textrm)-0\textrm,03 \textrm{pH}
Il reste à déterminer E°\textrm{(HClO/Cl}^-\textrm).
Méthode 1 :
On connaît un point de la droite E\textrm{(HClO/Cl}^-\textrm)=E°\textrm{(HClO/Cl}^-\textrm)-0\textrm,03 \textrm{pH}. C'est le point \textrm{A}(\mathrm{2,5} ;\mathrm{1,42}), donc 1\textrm,42=E°\textrm{(HClO/Cl}^-\textrm)-0\textrm,03\times2\textrm,5.
E°\textrm{(HClO/Cl}^-\textrm)=1\textrm,495 \textrm V
Méthode 2 :
Il est également possible de remonter à ce potentiel redox par la méthode présentée dans la partie diagramme de Frost :
n_1E°\textrm{(Cl}_2\textrm{/Cl}^-\textrm)+n_2E°\textrm{(HClO/Cl}_2\textrm)=n_3E°\textrm{(HClO/Cl}^-\textrm)
avec n_1=1,n_2=1 et n_3=2, d'où
E°\textrm{(HClO/Cl}^-\textrm)=\frac{n_1E°\textrm{(Cl}_2\textrm{/Cl}^-\textrm)+n_2E°\textrm{(HClO/Cl}_2\textrm)}{n_3}
E°\textrm{(HClO/Cl}^-\textrm)=\frac{1\times1\textrm,36+1\times1\textrm,63}{2}=1\textrm,495 \textrm V
Donc l'équation de la droite est : \textrm E\textrm{(HClO/Cl}^-\textrm)=1\textrm,495-0\textrm,03 \textrm{pH}

Frontière \textrm{CLO}^-\textrm{/Cl}^-
Cette frontière fait intervenir à la fois un changement de \textrm{pH} et de degré d'oxydation.
La réaction est :
\textrm{Cl}^{+\textrm I}+2.\textrm e^-+2.\textrm H^+\to\textrm{(ClO}^-\textrm)^{-\textrm I}+\textrm H_2\textrm O
E\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)+\frac{0,06}{2}\log\frac{[\textrm{ClO}^-][\textrm H^+]^2}{[\textrm{Cl}^-]}
avec par convention [\textrm{Cl}^-]+[\textrm{ClO}^-]=c_0 et [\textrm{Cl}^-]=[\textrm{ClO}^-] \Longrightarrow[\textrm{Cl}^-]=[\textrm{ClO}^-]=\frac{c_0}{2}
E\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)+\frac{0,06}{2}\log[\textrm H^+]^2
E\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)-0\textrm,06 \textrm{pH}
Il reste à déterminer E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)
Méthode 1 :
On connaît un point de la droite E\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)-0\textrm,06 \textrm{pH}.
C'est le point \textrm{B}(\mathrm{7,5} ;\mathrm{1,27}), donc 1\textrm,27=E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)-0\textrm,06\times7\textrm,5.
E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=1\textrm,72 \textrm V
Méthode 2 :
On peut écrire le cycle ci-dessous qui correspond aux équations chimiques suivantes :
\textrm{ClO}^-+\textrm H^+\to\textrm{HClO}\textrm{ } \textrm{ } \Delta_\textrm rG_1
\textrm{HClO}+2.\textrm e^-+\textrm H^+\to\textrm{Cl}^-+\textrm H_2\textrm O\textrm{ }\textrm{ }\Delta_\textrm rG_2
\textrm{ClO}^-+2.\textrm e^-+2.\textrm H^+\to\textrm{Cl}^-+\textrm H_2\textrm O\textrm{ }\textrm{ }\Delta_\textrm rG

\Delta_\textrm r\textrm G_1=-(-RT\ln K_a)=8\textrm,314\times298\times\ln10^{-7\textrm,5}=-42786
\Delta_\textrm rG_2=-E°(\textrm{HClO/Cl}^-)nF=-1\textrm,495\times2\times96500
\Delta_\textrm rG=\Delta_\textrm rG_1+\Delta_\textrm rG_2=E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)nF
Donc
E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=-\frac{\Delta_\textrm rG_1+\Delta_\textrm rG_2}{nF}
E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=-\frac{RT\ln K_a-E°\textrm{(HClO/Cl}^-\textrm)nF}{E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm){nF}}
E°\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=-\frac{8\textrm,314\times298\times\ln10^{-7\textrm,5}-1495\times2\times96500}{2\times96500}=\textrm{1,72 V}
Remarque :
Par ce type de cycle il est également possible de calculer le potentiel redox du couple \textrm{HClO/Cl}^-.
Donc la droite a pour équation E\textrm{(ClO}^-\textrm{/Cl}^-\textrm)=1\textrm,72-0\textrm,06 \textrm{pH}
