Nomenclature, Nature et Propriétés des solutions obtenues [Les Orbitales Atomiques]

- Nomenclature :

Le nombre quantique n permet de spécifier une couche électronique. Le nombre quantique l permet de décrire une sous couche électronique. La valeur de l sera codée par une lettre dans la nomenclature des orbitales. On utilisera :

Valeur de l	l=0	l=1	l=2	l=3	l=4	....
Type d'orbitale	orbitale s	orbitale p	orbitale d	orbitale f	orbitale g	....

Ceci est tout à fait compréhensible si l'on inspecte les fonctions analytiques des orbitales hydrogénoïdes telles qu'elles ont été définies à la fin du chapitre précédent.

- Notation

Seuls les nombres quantiques n et l entrent en jeu dans la notation des Orbitales Atomiques. On notera alors :

1s pour une orbitale associée à n=1 et l=0

2p pour une orbitale associée à n=2 et l=1

4f pour une orbitale associée à n=4 et l=3

...

- Nature

Intéressons nous à l'électron de l'atome d'hydrogène dans son état fondamental. Cet électron est caractérisé par une fonction d'onde de type '1s' de la forme :

Ψ (1 s) = C . e^{- r / a_{0}}

a₀ est une constante qui vaut 0,529 Å et C est une constante de normalisation. Cette fonction ne possède pas de partie angulaire, elle ne dépend que de la distance entre l'électron et le noyau, notée r. Par conséquent, elle possède une symétrie sphérique, ce qui est en accord avec ce que nous savons d'une orbitale 's'.

La constante de normalisation C permet de s'assurer que cet électron remplit au moins une condition indispensable : qu'il existe !

La traduction mathématique de cette existence se caractérise par le fait d'imposer à 100 % la probabilité de trouver l'électron, si on le cherche dans tout l'espace (soit une probabilité de 1 pour trouver l'électron dans une sphère de rayon infini).

La probabilité de trouver une particule dans tout l'espace se calcule par l'intégrale sur tout l'espace de la densité de probabilité radiale, en prenant soin d'exprimer la fonction d'onde dans les coordonnées sphériques :

∭^{\infty} dP = ∭^{\infty} Ψ {(x, y, z)}^{2} dV = ∭^{\infty} 4 π Ψ {(r, θ, ϕ)}^{2} r^{2} dr = 1

la résolution de cette équation permet d'identifier la valeur de la constante de normalisation de l'OA 1s de l'atome d'hydrogène. La fonction s'écrit alors :

Ψ (1 s) = \sqrt{\frac{1}{π . a_{0}^{3}}} . e^{- r / a_{0}}

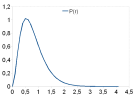
La densité de probabilité radiale P(r) de l'électron autour de son noyau va s'écrire:

P (r) = 4 π r^{2} Ψ^{2} = 4. \frac{r^{2}}{a_{0}^{3}} . e^{- 2. \frac{r}{a_{0}}}

pour obtenir le maximum de cette densité de probabilité radiale, il nous suffit de réaliser l'étude de cette fonction. Cette fonction sera maximale lorsque sa dérivée s'annule :

\frac{dP (r)}{dr} = 0

soit :

\frac{dP (r)}{dr} = \frac{8}{a_{0}^{3}} r e^{- 2 \frac{r}{a_{0}}} (1 - \frac{r}{a_{0}})

Cette fonction va s'annuler pour r = 0 ou pour r = a₀. On peut aussi voir que cette dérivée de P(r) est positive entre 0 et a₀, négative ensuite. P(r) est donc d'abord croissante jusque r = a₀, puis décroissante ensuite. La figure suivante montre l'évolution de P(r) en fonction de la distance r électron – noyau.

Si l'on cherche à connaître la probabilité de présence de l'électron à l'intérieur d'une sphère de rayon r, il s'agit d'intégrer P(r) entre 0 et r. Bien sur, cette probabilité va croître régulièrement, mais n'atteindra la valeur de 1 que pour une distance r infinie.

On fixe donc une valeur seuil de la valeur de r (r₉₅), généralement de 95 % de probabilité de présence, qui va correspondre à la distance que l'on appelle le rayon de l'orbitale atomique :

\int^{r_{95}} dP = 0,95

La résolution de cette équation mène à une valeur de r₉₅ = 3.a₀. On dit donc (abusivement) que la rayon de l'OA 1s de l'atome d'hydrogène est une sphère de rayon 3.a₀, soit à peu près 1,6 Å.

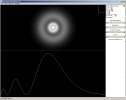
Cette procédure peut être appliquée à l'ensemble des OA hydrogénoïdes. Pour les OA 2s et 3s par exemple, la symétrie reste sphérique, mais on peut montrer que les probabilités de distribution radiales comportent des « nœuds », c'est à dire des zones de l'espace dans lesquelles les probabilités de trouver l'électron associé sont nulles.

La figure suivante illustre cette propriété. On distingue 1 nœud dans l'orbitale 2s et 2 nœuds dans l'orbitale 3s.

Le principe reste identique pour les orbitales qui contiennent une partie angulaire non-nulle, telles que les OA 'p' ou 'd'. L'étude de la partie radiale permet de connaître le nombre de nœuds de chacune d'elle.

Le site http://www.falstad.com/qmatom/ propose une application java qui permet de visualiser les orbitales atomiques hydrogénoïdes. La figure suivante illustre son utilisation pour l'OA 3s :

- Énergies

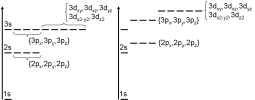
Dans le cadre de la résolution de l'équation de Schrödinger pour un atome hydrogénoïde, l'énergie ne dépend que du nombre quantique principal n. Les solutions énergétiques sont alors dites dégénérées, i.e. les niveaux sont à la même valeur pour un n donné, quelque soient les valeurs de l et m.

Dans le cadre du traitement d'un système poly-électronique, cette dégénérescence accidentelle disparaît et l'énergie s'exprime alors en fonction de l et m. Les solutions peuvent toujours s'écrire sous la forme : R_n,l(r).Y_l,m(\(\theta\),\(\Phi\)), seule l'expression des parties radiales étant modifiée.

Ainsi, à gauche nous voyons les niveaux énergétiques tels qu'ils apparaissent dans le cadre d'un atome hydrogénoïde. A droite, tels qu'ils apparaîtraient dans le cadre d'un atome polyélectronique. Dans ce nouveau cadre, on note une levée de dégénérescence qui correspond à une différence d'énergie entre les niveau 2s/2p d'un coté, 3s/3p/3d ensuite...

Ce point est important car il va avoir un impact sur la distribution électronique autour d'un noyau atomique, les niveaux les plus bas en énergie devant toujours être peuplés les premiers. Les structures électroniques que l'on utilise par la suite dérivent de cet aspect.

Malgré tout, il persiste un phénomène de dégénérescence, notamment au niveau des orbitales de type p et de type d (il en sera de même pour les orbitales de type f, g...)