2/ Localisation d'orbitales - Orbitales localisées de BeH2 [L'opérateur hamiltonien]

2/ Localisation d'orbitales - Orbitales localisées de BeH2

Partie

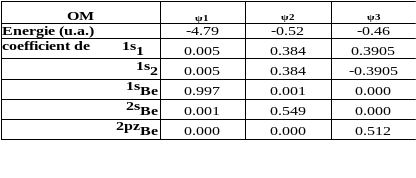
Un calcul sur la molécule BeH₂ a donné pour résultat les coefficients des Orbitales Atomiques pour trois Orbitales Moléculaires. (Z_Be = 4).

La molécule BeH₂ est linéaire. Les atomes sont donc répartis le long d'un axe selon :

La molécule est symétrique et l'axe choisit est nécessairement z d'après les données du tableau. En négligeant la participation des orbitales atomiques associées à des faibles valeurs de coefficients, les orbitales moléculaires s'écrivent:

\begin{matrix} Ψ_{1} = 0,997 . 1 s_{Be} \approx 1 s_{Be} \\ Ψ_{2} = 0,384 . 1 s_{1} + 0,384 . 1 s_{2} + 0,549 . 2 s_{Be} \\ Ψ_{3} = 0,3905 . 1 s_{1} - 0,3905 . 1 s_{2} + 0,512 . 2 {pz}_{Be} \end{matrix}

L'orbitale \(\Psi\) ₁correspond clairement à l'orbitale de cœur du Be et ne joue aucun rôle dans les modes de liaison entre le Be et les atomes d'hydrogène.

Question

Dessiner schématiquement les orbitales moléculaires \(\Psi\) ₁, \(\Psi\) ₂et \(\Psi\) ₃

Solution détaillée

Parmi ces trois orbitales moléculaires, deux doivent représenter des modes de liaison (orbitales moléculaires liantes) car l'atome de Be doit être lié à deux atomes d'hydrogène.

En considérant que les différences de signes mathématiques peuvent être représentés par des couleurs différentes (par exemple rouge : positif et bleu : négatif), nous pouvons schématiser comme suit les orbitales moléculaires :

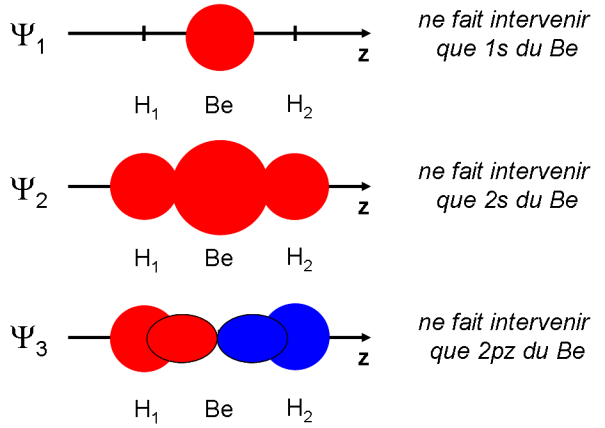
Dans Y3, nous avons clairement choisi « d'inverser » le signe de l'orbitale 2pz du Be tel qu'il aurait pu être anticipé au départ de telle façon à créer une orbitale moléculaire liante. Ce choix est compatible avec les orbitales moléculaires présentes dans BeH2 et cohérent avec les énergies données dans le tableau.

Question

On définit la transformation :

\begin{matrix} Ψ'_{2} = \cos (γ) . Ψ_{2} + \sin (γ) . Ψ_{3} \\ Ψ'_{3} = - \sin (γ) . Ψ_{2} + \cos (γ) . Ψ_{3} \end{matrix}

Quelle valeur de \(\gamma\) faudrait-il choisir pour que le coefficient de 1s2 soit nul dans \(\Psi\) '₂. Même question pour que le coefficient de 1s1 soit nul dans \(\Psi\) '₃

Solution détaillée

Considérons tout d'abord la recherche de \(\gamma\) pour annuler la contribution de 1s2 dans \(\Psi\) '₂ : en remplaçant par les coefficients du tableau, \(\Psi\) '₂ s'écrit :

\begin{matrix} Ψ'_{2} = \cos (γ) . [0,384 . 1 s_{1} + 0,384 . 1 s_{2} + 0,549 . 2 s_{Be}] \\ + \sin (γ) . [0,3905 . 1 s_{1} - 0,3905 . 1 s_{2} + 0,512 . 2 {pz}_{Be}] \\ Ψ'_{2} = [\cos (γ) . 0,384 . + \sin (γ) . 0,3905 .] 1 s_{1} \\ + [\cos (γ) . 0,384 - \sin (γ) . 0,3905] . 1 s_{2} \\ + \cos (γ) . 0,549 . 2 s_{Be} + \sin (γ) . 0,512 . 2 {pz}_{Be} \end{matrix}

afin d'annuler la contribution de 1s2 dans \(\Psi\) '₂ il faut que son coefficient soit nul, ce qui mène à :

\begin{matrix} \cos (γ) . 0,384 - \sin (γ) . 0,3905 = 0 \\ soit \\ tg (γ) = \frac{0,384}{0,3905} \\ ou encore \\ γ = 44,52 ° \end{matrix}

Considérons maintenant la recherche de \(\gamma\) pour annuler la contribution de 1s1 dans \(\Psi\) '₃' : en remplaçant par les coefficients du tableau, \(\Psi\) '₃ s'écrit :

\begin{matrix} Ψ'_{3} = - \sin (γ) . [0,384 . 1 s_{1} + 0,384 . 1 s_{2} + 0,549 . 2 s_{Be}] \\ + \cos (γ) . [0,3905 . 1 s_{1} - 0,3905 . 1 s_{2} + 0,512 . 2 {pz}_{Be}] \\ Ψ'_{3} = [- \sin (γ) . 0,384 . + \cos (γ) . 0,3905 .] 1 s_{1} \\ + [- \sin (γ) . 0,384 + \cos (γ) . 0,3905] . 1 s_{2} \\ - \sin (γ) . 0,549 . 2 s_{Be} + \cos (γ) . 0,512 . 2 {pz}_{Be} \end{matrix}

afin d'annuler la contribution de 1s1 dans \(\Psi\) '₃ il faut que son coefficient soit nul, ce qui mène à :

\begin{matrix} - \sin (γ) . 0,384 + \cos (γ) . 0,3905 = 0 \\ soit \\ tg (γ) = \frac{0,3905}{0,384} \\ ou encore \\ γ = 45,48 ° \end{matrix}

Les deux valeurs ne sont pas égales (\(\gamma\)=44,52 degrés et \(\gamma\)=45,48 degrés), donc les deux conditions ne pourraient être assurées en même temps. En revanche, si l'on considère que des erreurs numériques ont pu apparaître dans le tableau, qui auraient pu engendrer des erreurs numériques dans la détermination des valeurs de \(\gamma\), alors, on peut considérer qu'une valeur approchée de \(\gamma\), permettant de répondre au plus près au deux conditions pourrait être acceptable.

\(\gamma\)=45 degrés semble bien répondre à cette condition.

Question

Ecrire les expressions analytiques des orbitales \(\Psi\) '₂ et \(\Psi\) '₃ avec g=45 degrés.

Solution détaillée

\begin{matrix} Ψ'_{2} = [\cos (45) . 0,384 . + \sin (45) . 0,3905 .] 1 s_{1} \\ + [\cos (45) . 0,384 - \sin (45) . 0,3905] . 1 s_{2} \\ + \cos (45) . 0,549 . 2 s_{Be} + \sin (45) . 0,512 . 2 {pz}_{Be} \\ Ψ'_{2} = [\frac{\sqrt{2}}{2} . 0,384 . + \frac{\sqrt{2}}{2} . 0,3905 .] 1 s_{1} \\ + [\frac{\sqrt{2}}{2} . 0,384 - \frac{\sqrt{2}}{2} . 0,3905] . 1 s_{2} \\ + \frac{\sqrt{2}}{2} . 0,549 . 2 s_{Be} + \frac{\sqrt{2}}{2} . 0,512 . 2 {pz}_{Be} \\ Ψ'_{2} = 1,41 . 1 s_{1} - 0,005 . 1 s_{2} + 0,39 . 2 s_{Be} + 0,36 . 2 {pz}_{Be} \\ et \\ Ψ'_{3} = [- \sin (45) . 0,384 . + \cos (45) . 0,3905 .] 1 s_{1} \\ + [- \sin (45) . 0,384 - \cos (45) . 0,3905] . 1 s_{2} \\ - \sin (45) . 0,549 . 2 s_{Be} + \cos (45) . 0,512 . 2 {pz}_{Be} \\ Ψ'_{3} = [\frac{- \sqrt{2}}{2} . 0,384 . + \frac{\sqrt{2}}{2} . 0,3905 .] 1 s_{1} \\ + [\frac{- \sqrt{2}}{2} . 0,384 - \frac{\sqrt{2}}{2} . 0,3905] . 1 s_{2} \\ - \frac{\sqrt{2}}{2} . 0,549 . 2 s_{Be} + \frac{\sqrt{2}}{2} . 0,512 . 2 {pz}_{Be} \\ Ψ'_{3} = - 0,005 . 1 s_{1} - 1,41 . 1 s_{2} - 0,39 . 2 s_{Be} + 0,36 . 2 {pz}_{Be} \end{matrix}

En négligeant les orbitales atomiques associées à des faibles valeurs de coefficients :

\begin{matrix} Ψ'_{2} = 1,41 . 1 s_{1} + 0,39 . 2 s_{Be} + 0,36 . 2 {pz}_{Be} \\ Ψ'_{3} = - 1,41 . 1 s_{2} - 0,39 . 2 s_{Be} + 0,36 . 2 {pz}_{Be} \end{matrix}

Question

Dessiner schématiquement les orbitales obtenues.

Solution détaillée

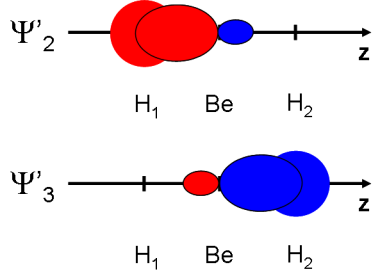
Nous avons créé deux orbitales moléculaires localisées, chacune décrivant une des deux liaison BeH. La matrice de transformation qui a été appliquée est une matrice de rotation.