Invariants du mouvement
Certaines grandeurs physiques scalaires et vectorielles se conservent au cours du mouvement. Elles servent alors à caractériser le mouvement. On les appelle invariants ou constantes du mouvement.
Grandeur physique scalaire
Dans le cas où les forces dérivent d'une énergie potentielle (système conservatif), l'énergie totale \(\mathrm E\) est constante :
L'énergie totale d'un ensemble de particules en interaction est constante dans l'espace et au cours du temps.
Grandeur physique vectorielle
Considérons la grandeur physique vectorielle appelée moment cinétique
\(\mathbf{\overrightarrow l=\overrightarrow r\land\overrightarrow p=\overrightarrow r\land m.\overrightarrow v}\)
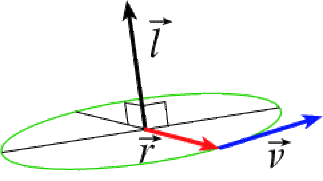
Ses coordonnées sont :
\(\mathrm{l_x=y.p_z-z.p_y}\)
\(\mathrm{l_y=z.p_x-x.p_z}\)
\(\mathrm{l_z=x.p_y-y.p_x}\)
Cette grandeur physique est un invariant du mouvement dans le cas de force centrale.
Il y a force centrale quand la force s'exerçant sur la particule ne dépend que de sa distance à un point fixe ; par exemple quand on décrit le mouvement d'une planète soumise au champ gravitationnel central du soleil ou encore celui d'un électron soumis au champ coulombien central du noyau atomique.