Maille élémentaire
La maille élémentaire est définie par trois vecteurs élémentaires \(\vec a\) ,\(\vec b\) et \(\vec c\) de modules \(\textrm a\), \(\textrm b\) et \(\textrm c\) respectivement.
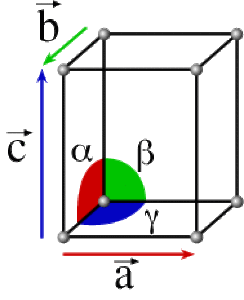
Les angles entre ces vecteurs sont \(\alpha\) , \(\beta\) et \(\gamma\).
\(\alpha\) est l'angle entre les vecteurs \(\vec b\) et \(\vec c\)
\(\beta\) est l'angle entre les vecteurs \(\vec a\) et \(\vec c\)
\(\gamma\) est l'angle entre les vecteurs \(\vec a\) et \(\vec b\)
\(\textrm a\), \(\textrm b\) et \(\textrm c\) et les angles \(\alpha\), \(\beta\) et \(\gamma\) sont les paramètres de maille.
Une maille élémentaire peut être simple ou multiple. Une maille simple contient un groupement formulaire, une maille multiple peut contenir plusieurs groupements. Le nombre de groupements formulaires est appelé multiplicité de la maille.
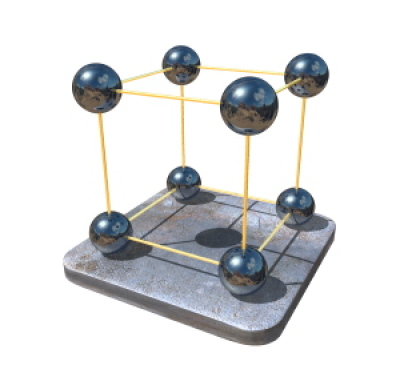
maille simple cubique

maille multiple cubique
La multiplicité ou nombre de groupements formulaires \(\textrm Z\) est défini comme le rapport de la masse de la maille sur la masse du groupement formulaire. On peut obtenir la multiplicité d'une maille à partir de son volume \(\textrm V\), du nombre d'Avogadro \(\textrm N_\textrm A\), de la masse volumique \(\rho\) du cristal et de la masse molaire \(\textrm M\) du composé.
La masse de la maille est \(\rho\times \textrm V\), la masse d'un groupement formulaire est \(\frac{\textrm M}{\textrm N_\textrm A}\). Il vient alors :
\(\mathbf{Z=\frac{\rho.V.\textrm N_\textrm A}{\textrm M}}\)