Le fer
Durée : 5 mn
Note maximale : 4
Question
Le fer\(\alpha\)cristallise dans le système cubique centré avec un paramètre de maille\(\textrm{a} = \mathrm{2,87}~\AA\). On envoie un faisceau de rayons\(\textrm{X}\)de longueur d'onde\(\lambda = \mathrm{1,54}~\AA\)sur un échantillon de fer\(\alpha\). Pour un angle de diffraction\(\theta = \mathrm{32,58}°\), on obtient une diffraction de premier ordre due à une famille de plans parallèles à une face de la maille.
Calculer la distance réticulaire et expliquer votre résultat.
Solution
On applique la relation de Bragg.
\(2~d~\sin\theta = k~\lambda\)avec\(k = 1\)
\(d = \frac{\lambda}{2~\sin\theta} = \frac{\mathrm{1,54}}{2~\sin~(\mathrm{32,58})} = \mathrm{1,43}~\AA\)
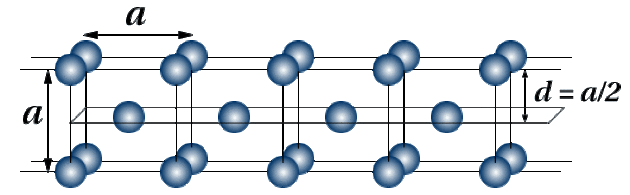
On constate que la distance mesurée est la moitié du paramètre de maille. Les plans qui diffractent correspondent aux faces du cube et aux plans formés par les atomes du centre de la maille, comme indiqué sur la figure ci-dessous.