Le fer
Durée : 12 mn
Note maximale : 3
Question
Le fer\(\gamma\)cristallise dans le système cubique à faces centrées avec un paramètre de maille\(\textrm{a} = \mathrm{3,65}~\AA\). On envoie un faisceau de rayons\(\textrm{X}\)sur un échantillon de fer\(\gamma\). Les plans qui diffractent sont perpendiculaires à la direction de la grande diagonale du cube. L'angle de diffraction est\(\theta = \mathrm{9,71}°\). La distance entre les plans réticulaires est\(\textrm{d} = \mathrm{2,107}~\AA\).
Identifier la famille de plans qui diffracte (on la désignera sur une figure appropriée de la maille).
Quelle est la longueur d'onde du rayonnement utilisé ?
Solution
1. Pour visualiser les plans qui diffractent, on peut représenter la maille et voir que ces plans correspondent aux plans ABC indiqués sur la figure ci-dessous.
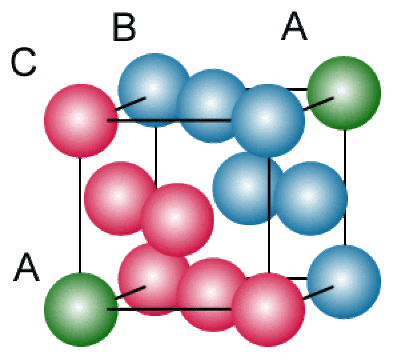
La longueur de la grande diagonale vaut\(\textrm{a}\sqrt{3}\),soit\(\mathrm{6,322}~\AA\). La distance entre les plans est :\(\qquad\) \(d = \frac{\textrm{a}\sqrt{3}}{3} = \mathrm{2,107}~\AA\)
2. On applique la relation de Bragg au premier ordre :\(\qquad\) \(\lambda = 2~d~\sin\theta = 2~\times~\mathrm{2,107}~\times~\sin(\mathrm{9,71}) = \mathrm{0,7104}~\AA\)