Théorème de Bolzano-Weierstrass
Une suite convergente est bornée, la réciproque est fausse mais le théorème de Bolzano-Weirstrass exprime qu'une suite bornée admet une suite extraite convergente. Le théorème de Bolzano- Weierstrass est un "grand" théorème non seulement parce que son rôle est fondamental dans l'étude globale des fonctions mais parce que, pour une suite \((u_n)\) réelle, la propriété \((u_n)\) est bornée étant équivalente à \((u_n)\) prend ses valeurs dans un intervalle fermé borné de \(\mathbb R\), le théorème de Bolzano- Weierstrass caractérise une propriété des intervalles fermés bornés de \(\mathbb R\) la compacité.
Théorème :
De toute suite réelle bornée on peut extraire une sous-suite convergente.
Preuve :
On construit la suite extraite par dichotomie c'est à dire en coupant successivement en 2, les intervalles contenant une infinité de termes de la suite.
Il s'agit d'une démonstration par dichotomie.
Soit \((u_n)\) une suite réelle bornée et soient \(a \textrm{ et }b\) deux réels tels que l'on ait, pour tout entier \(n : a\leq u_n \leq b\): tous les termes de la suite appartiennent à l'intervalle fermé et borné \([a,b]\).
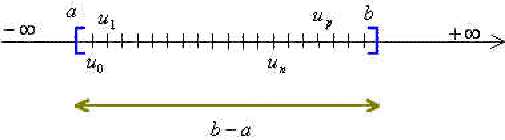
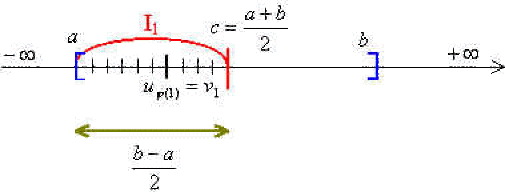
On pose \(\displaystyle{c=\frac{a+b}{2}}\) et on considère les deux intervalles fermés bornés \([a,c] \textrm{ et }[c,b]\). Des deux ensembles \(\displaystyle{\{n\in\mathbb N,u_n\in[a,c]\}\textrm{ et }\{n\in\mathbb N,u_n\in[c,b]\}}\) l'un au moins est infini. On désigne par \(I_1\) celui des deux intervalles qui contient une infinité de termes de la suite et par \(\phi(1)\) le plus petit entier tel que \(u_{\phi(1)}\) appartienne à \(I_1\) (dans le cas où les deux intervalles contiennent une infinité de termes on en choisit arbitrairement un). La longueur de \(I_1\) est égale à \(\displaystyle{\frac{b-a}{2}}\) et l'ensemble \(\displaystyle{\{n\in\mathbb N,u_n\in I_1\}}\) est infini. On pose \(\displaystyle{v_1=u_{\phi(1)}}\).
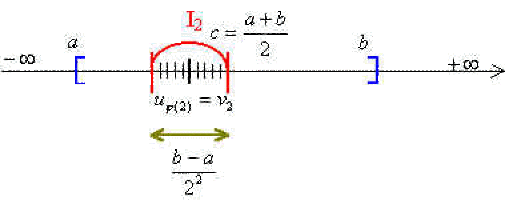
On recommence alors sur \(I_1\) ce qui a été fait sur \(I\); en considérant le milieu de \(I_1\) on fait apparaitre deux intervalles dont l'un, au moins, contient une infinité de termes de la suite . On désigne par \(I_2\) cet intervalle et par \(\phi(2)\) le plus petit entier strictement supérieur à \(\phi(1)\) tel que \(u_{\phi(2)}\)appartienne à \(I_2\).
La longueur de \(I_2\) est égale à \(\frac{b-a}{2^2}\); on pose \(v_2=u_{\phi(2)}\).
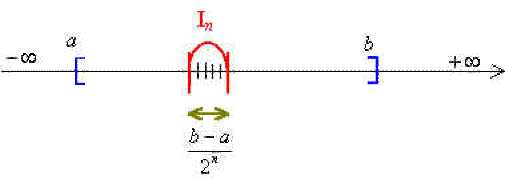
On définit par récurrence une suite d'intervalles \((I_n)\) et une suite \((v_n)=(u_{\phi(n)})\) de réels extraite de la suite \((u_n)\) telles que :
\(\displaystyle{I_0=[a,b]\textrm{ et }v_0=u_0}\)
pour tout entier \(n\), on définit \(I_{n+1}\) à partir de \(I_n\) par les conditions :
\(\displaystyle{I_{n+1}\subset I_n}\) et la longueur de \(I_{n+1}\) est la moitié de celle de \(I_n\)
\(I_{n+1}\) contient une infinité de termes de la suite \((u_n)\)
et \((v_n)=(u_{\phi(n)})\) par les conditions :
la fonction \(\phi\) est strictement croissante
\(\displaystyle{u_{\phi(n+1)}\in I_{n+1}}\)
La suite \((v_n)=(u_{\phi(n)})\) est extraite de la suite \((u_n)\). De plus la longueur de \(I_n\) est égale à \(\displaystyle{\frac{b-a}{2^n}}\). On montre que la suite \((v_n)\) est de Cauchy.
Soit \(\epsilon\) un réel strictement positif et soit \(N\) un entier tel que \(\displaystyle{\frac{b-a}{2^{N}}<\epsilon}\). Pour tout entier \(n\geq N\) on a \(\displaystyle{v_n\in I_n\subset I_{N}}\) , d'où, pour tout couple d'entiers \((p,n)\) vérifiant \(p\geq N\) et \(n\geq N\),
\(\displaystyle{\left\vert v_p-v_n\right\vert\leq\frac{b-a}{2^{N}}<\epsilon}\)
On a donc construit une suite extraite de la suite \((u_n)\) qui est une suite de Cauchy et donc convergente.
Remarque :
Autre preuve se basant sur les suites adjacentes
Au lieu de faire appel au théorème de Cauchy, on peut aussi, une fois construites la suite d'intervalles \((I_n)\) et la suite \((v_n)\) , noter \(a_n \textrm{ et }b_n\) les bornes de l'intervalle \(I_n\) et considérer les suites \((a_n) \textrm{ et }(b_n)\):
la suite \((a_n)\) est croissante, la suite \((b_n)\) est décroissante,
pour tout entier \(n\), on a \(a_n\le b_n\),
pour tout entier \(n\), on a \(\displaystyle{b_n-a_n=\frac{b-a}{2^n}}\)
Les suites \((a_n) \textrm{ et }(b_n)\) sont donc adjacentes, elles sont donc convergentes et ont même limite.
Pour terminer la démonstration, il suffit de remarquer que, pour tout entier \(n\), on a
\(a_n\leq v_n\leq b_n\)
ce qui entraine que la suite \((v_n)\) est convergente et a même limite que les suites \((a_n) \textrm{ et }(b_n)\).
Il est à noter que dans les deux cas (théorème de Cauchy ou suites adjacentes) l'hypothèse que la suite \((u_n)\) est une suite bornée de nombres réels est essentielle. On utilise les bornes \(a \textrm{ et }b\) pour mettre en place la récurrence et le fait qu'on est dans \(\mathbb R\) assure :
soit la convergence de la suite de Cauchy \((v_n)\)
soit la convergence des deux suites \((a_n) \textrm{ et }(b_n)\).