Fonctions convexes dérivables
Lemme :
Soit \(f\) une fonction convexe et dérivable sur un intervalle\( \mathcal I\) de \(\mathbf R\) . Si \(a\) est un point intérieur à \(\mathcal I\), on a :
\(\displaystyle{\forall x\in\mathcal I,x< a\quad r_a(x)\leq f'(a)}\)
\(\displaystyle{\forall x\in\mathcal I,x> a\quad r_a(x)\geq f'(a)}\)
Preuve :
Il s'agit d'une conséquence immédiate du théorème précédent.
Théorème :
Soit \(f\) une fonction dérivable sur \(\mathcal I\) ; alors \(f\) est convexe sur \(\mathcal I\) si et seulement si \(f'\) est croissante sur \(\mathcal I\).
Preuve :
On utilise le lemme pour la condition nécessaire et le théorème des accroissements finis pour la condition suffisante.
Condition nécessaire:
On suppose \(f\) dérivable et convexe sur \(I\), d’après le lemme précédent, on a : \(\forall x_1\in I,\forall x_2\in I,x_1<x_2\Rightarrow(f'(x_1)\le r_{x_1}(x_2)~\textrm{et}~r_{x_2}(x_1)\le f'(x_2))\).
Or \(r_{x_2}(x_1)=r_{x_1}(x_2)\) d'où \(f'(x_1)\le f'(x_2)\).
Condition suffisante :
Quels que soient \((x_1,x_2)\in I^2,x_1<x_2\), et \(\lambda\in]0,1[\), on pose : \(x=\lambda x_1+(1-\lambda)x_2\).
On a alors \(x_1 < x < x_2\) ; d’après le théorème des accroissements finis il existe \(c_1\in]x_1,x[\) et \(c_2\in]x,x_2[\) tels que : \(f(x)-f(x_1)=(x-x_1)f'(c_1)\) et \(f(x_2)-f(x)=(x_2-x)f'(c_2)\).
L’inégalité \(c_1< c_2\) entraine alors \(f'(c_1)\le f'(c_2)\) soit \(\frac{f(x)-f(x_1)}{x-x_1}\le\frac{f(x_2)-f(x)}{x_2-x}\).
Des égalités \(x-x_1=(1-\lambda)(x_2-x_1)\) et \(x_2-x=\lambda(x_2-x_1)\) on déduit : \(f(\lambda x_1+(1-\lambda)x_2)\le\lambda f(x_1)+(1-\lambda)f(x_2)\) ;
ceci étant vrai quels que soient \((x_1,x_2)\in I^2\) et \(\lambda\in]0,1[\), la fonction \(f\) est convexe.
Corollaire :
Soit \(f\) une fonction deux fois dérivable sur \(\mathcal I\) ; \(f\) est convexe sur \(\mathcal I\) si et seulement si \(f''\) est positive sur \(\mathcal I\). Si \(f''\) est négative sur \(\mathcal I\) alors \((-f)\) est convexe et donc \(f\) est concave.
Preuve :
Immédiat
Exemple :
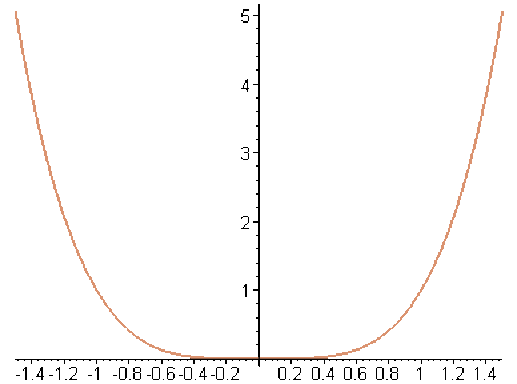
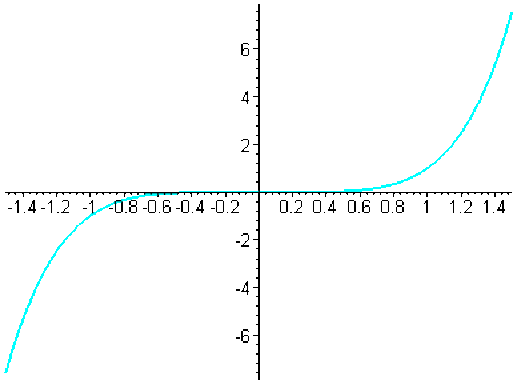
les fonctions \(x\mapsto x^n (n\in\mathcal N)\) sont convexes sur \(\mathbf R\) si \(n\) est pair, elles sont concaves sur\( ]-\infty,0]\) et convexes sur \([0,+\infty[\) si est \(n\) impair ,
n=4
n=5
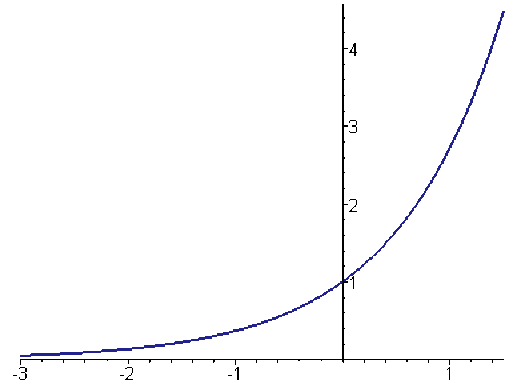
la fonction exponentielle est convexe sur \(\mathbf R\),
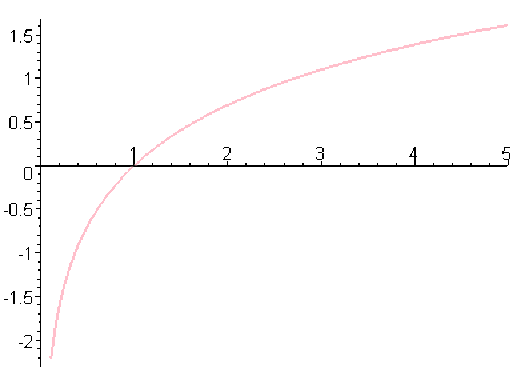
la fonction logarithme est concave sur \(]0,+\infty]\),