Existence et détermination d'une application réciproque
Durée : 15 mn
Note maximale : 10
Question
Soit la fonction \(f\) définie par : \(x \mapsto f(x) = \frac{x}{\sqrt{4-x^2}}\)
Faire l'étude complète de \(f\) et construire son graphe dans un repère orthonormé. (4 pts)
Démontrer que \(f\) définit une bijection d'un intervalle \(\mathbb I\) sur \(\mathbb R\) et déterminer sa bijection réciproque. (4 pts)
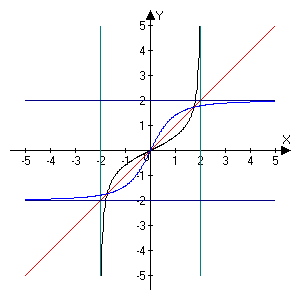
Construire le graphe de \(f^{-1}\)dans le même repère que celui de \(f.\) (2 pts)
Solution
1. (4 pts) L'expression \(f(x) = \frac{x}{\sqrt{4-x^2}}\)est définie sur l'ensemble des réels \(x\) tels que \(4-x^2 >0,\) c'est-à-dire l'intervalle \(\mathbb I=]-2,2[.\)
La fonction \(f\) est impaire, son graphe admet l'origine pour centre de symétrie.
La fonction \(f\) est continue et dérivable sur \(\mathbb I,\) car la fonction \(x\mapsto 4-x^2\)est continue, dérivable et strictement positive sur \(\mathbb I.\)
Pour tout \(x\) élément de \(\mathbb I\) on peut écrire \(f(x) = x(4-x^2)^{-\frac{1}{2}},\) d'où
\(\forall x \in ]-2,2[~~f'(x)=-\frac{1}{2}(-2x)(4-x^2)^{-\frac{3}{2}}x+(4-x^2)^{-\frac{1}{2}}=\frac{4}{(4-x^2)^{\frac{3}{2}}}\)
La fonction \(f\) est donc strictement croissante sur \(\mathbb I.\)
Quand \(x\) tend vers \(2\) par valeurs inférieures, \(f(x)\)tend vers \(+\infty\): \(\lim_{x\rightarrow2,x<2}f(x)=+\infty.\)
La fonction \(f\) étant impaire, on a \(\lim_{x\rightarrow-2,x>-2}f(x)=-\infty\)
Le graphe de \(f\) admet donc deux asymptotes, parallèles à l'axe \(y'y,\) d'équations \(x=2\) et \(x=-2.\)
2. (4 pts) La fonction \(f\) étant continue et strictement croissante sur l'intervalle \(\mathbb I,\) l'image par \(f\) de \(\mathbb I\) est l'intervalle \(]-\infty,+\infty[\)c'est-à-dire \(\mathbb R\) et \(f\) définit une bijection de \(\mathbb I\) sur \(\mathbb R.\)
\(x\) étant élément de \(]-2,2[,\) on a l'équivalence : \(y=f(x)\Leftrightarrow x=f^{-1}(y).\)
Etant donné \(y\) réel, on cherche \(x\) élément de \(]-2, 2[,\) tel que \(f(x)=y.\)
Il s'agit donc de résoudre l'équation \((E)~~\frac{x}{\sqrt{4-x^2}} = y\)
L'équation obtenue en élevant au carré les deux membres : \(\frac{x^2}{4-x^2}=y^2,\) n'est pas équivalente à \((E),\) car on a perdu l'information \("x\) et \(y\) sont de même signe".
Donc \((E)~~\Leftrightarrow~~\begin{cases}x^2=y^2(4-x^2)\\xy\geq0\end{cases}~~\Leftrightarrow \begin{cases}x^2=\frac{4y^2}{y^2+1}\\xy\geq 0\end{cases}\)
La condition \(xy \geq 0\)permet d'éliminer la solution \(x=\frac{-2y}{\sqrt{y^2+1}}.\)
L'unique solution est donc : \(x=f^{-1}(y)=\frac{2y}{\sqrt{y^2+1}}.\)
Vérifions que \(x\) est bien élément de \(]-2,2[\): pour tout réel \(y,~\sqrt{y^2+1}>|y| ,\) donc \(|\frac{2y}{\sqrt{y^2+1}}| < 2.\)
D'où : \(\begin{array}{r c l}f^{-1} :\mathbb R & \rightarrow & ]-2,2[ \\x & \mapsto & \frac{2x}{\sqrt{x^2+1}}\end{array}\)
3. (2 pts) Le graphe de \(f^{-1}\)s'obtient à partir de celui de \(f\) par la symétrie par rapport à la première bissectrice (d'équation \(y=x)\)
Sur la figure ci-contre, le graphe de \(f\) est en noir et celui de \(f^{-1}\)est en bleu.
