Racine nième d'un réel positif
On se pose la question : "Une fonction du type \(x \mapsto x^n~~(n \in \mathbb N ^*)\) admet-elle une fonction réciproque ?", plus précisément "Peut-on lui appliquer le théorème des fonctions réciproques ?".
Théorème : des fonctions réciproques
Soit \(f\) une fonction continue strictement monotone sur un intervalle \(I.\) Alors
1) \(f(I)\) est un intervalle \(J\) de même nature que \(I\) (fermé, ouvert ou semi ouvert) et ses extrémités sont les limites de\( f\) aux extrémités de \(I.\)
2) La fonction \(f\) admet une fonction réciproque définie sur \(J = f(I)\); plus précisément, \(f\) définit une bijection de l'intervalle \(I\) sur l'intervalle \(J,\) donc il existe une fonction notée \(f^{-1}~\textrm{de}~J\) dans \(I,\) telle que
\(\begin{array} {|l|}\hline x \in I\\ y = f(x) \\ \hline \end{array} ~~\Leftrightarrow~~\begin{array} {|l|}\hline y \in J\\ x = f^{-1}(y) \\ \hline \end{array}\)
3) La fonction réciproque \(f^{-1}\)est continue et strictement monotone sur \(J,\) de même sens de monotonie que \(f.\)
4) De plus, si \(f\) est dérivable en un point \(x_0\) de \(I\) et si \(f'(x_0)\)est non nul, \(f^{-1}\)est dérivable au point \(y_0 = f(x_0)~\textrm{et}~(f^{-1})'(y_0) = \frac{1}{f'(x_0)} = \frac{1}{f'(f^{-1}(y_0))}.\)
L'étude précédente montre que ces fonctions ne sont pas toutes strictement monotones sur \(\mathbb R.\) En revanche, pour tout entier naturel \(n,\) non nul, la restriction à \(\mathbb R ^+\) de la fonction \(x \mapsto x^n\)est continue strictement croissante sur \(\mathbb R ^+,\) l'image de \(0\) est \(0\) et la limite en \(+\infty\) est \(+\infty\): c'est donc une bijection continue de \(\mathbb R ^+\) sur lui même et elle admet une bijection réciproque.
On fait le choix d'appliquer le théorème des fonctions réciproques à la fonction \(\begin{array}{ l c r }\mathbb R^+ & \rightarrow & \mathbb R^+ \\x & \mapsto & x^n \\\end{array}\)
Sa fonction réciproque est appelée racine \(n^{ieme},\) qui est notée \(\begin{array}{ l c r }\mathbb R^+ & \rightarrow & \mathbb R^+ \\x & \mapsto & \sqrt[n]{x} \\\end{array}\)
Pour résumer, on a :
\(\begin{array} {|l|}\hline y = \sqrt[n]{x}\\ x \in \mathbb R ^+ \\ \hline \end{array}~~\Leftrightarrow~~\begin{array} {|l|}\hline x = y^n\\ y \in \mathbb R ^+ \\ \hline \end{array}\)
Autrement dit, si \(x\) est un réel positif, \(\sqrt[n]{x}\) est l'unique réel positif qui, élevé à la puissance \(n,\) vaut \(x.\)
Remarque :
L'entier \(n\) est l'indice du radical, il est omis lorsqu'il est égal à 2 : on écrit\(\sqrt{x}\) au lieu de \(\sqrt[2]{x}.\)
On notera que pour \(n = 1, \sqrt[1]{x} = x.\)
D'après le théorème des fonctions réciproques, la fonction \(f : x \mapsto x^n\)étant continue et strictement croissante sur \(\mathbb R ^+,\) il en est de même pour \(f^{-1} : x \mapsto \sqrt[n]{x}.\)
La fonction \(f : x \mapsto x^n \)est dérivable sur \([0, +\infty[,\) sa dérivée est \(f' : x \mapsto nx^{n-1},\) elle s'annule pour \(x=0\)sauf dans le cas où \(n =1.\)
Par conséquent, pour \(n \geq 2,\) la fonction \(f^{-1} : x \mapsto \sqrt[n]{x}\)est dérivable sur \(]0, +\infty[,\) et sa dérivée est :
\((f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{n(\sqrt[n]{x})^{n-1}}\)
Par exemple, la fonction dérivée de \(x \mapsto \sqrt{x}\)est \(x \mapsto \frac{1}{2\sqrt{x}}.\)
Le cas où \(n = 1\)est trivial puisque la fonction réciproque de \(x \mapsto x\)est \(x \mapsto x\)!
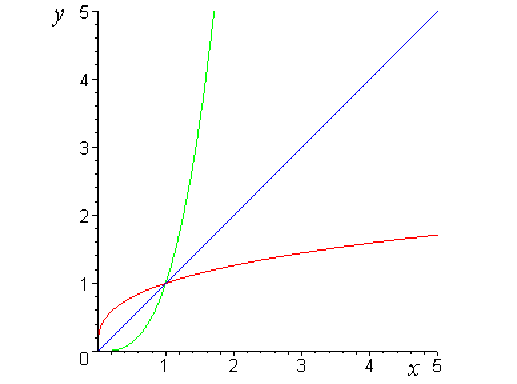
Dans un même repère orthonormé, le graphe de \(x\mapsto \sqrt[n]{x}\)se déduit de celui de \(x \mapsto x^n\)par la symétrie par rapport à la première bissectrice (d'équation \(y=x\)).
Exemple
\(\color{green} x \mapsto x^3\)
\(\color{red} x \mapsto \sqrt[3]{x}\)
\(\color{blue} x \mapsto x\)
Propriété :
Pour tout réel positif \(a\) et pour tout entier \(n\) strictement positif on a :
\((\sqrt[n]{a})^n = a\)
\(\sqrt[n]{a^n} = a\)
Ceci découle simplement du fait que les fonctions \(x \mapsto x^n~\textrm{et}~x \mapsto \sqrt[n]{x}\) sont réciproques l'une de l'autre.
Attention !
Dans le cas où \(n\) est pair, c'est à dire \(n = 2p,~a^{2p}\) est toujours positif, donc \(\sqrt[2p]{a^{2p}}\)est défini pour tout réel \(a\) et on a :
\(\forall a \in \mathbb R~~\sqrt[2p]{a^{2p}} = |a|\)
En particulier, \(\forall a \in \mathbb R~~\sqrt{a^2} = |a|,\) c'est-à-dire si \(a \geq 0~\sqrt{a^2} = a,~\textrm{et si}~a \leq 0~\sqrt{a^2} = -a\).
Opérations sur les radicaux
Soient \(a~\textrm{et}~b\) deux réels positifs, \(n~\textrm{et}~p\) deux entiers strictement positifs, et \(k\) un entier quelconque. On a les propriétés suivantes :
\(\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}~~(1)\)
\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}~~(b \neq 0)~~(2)\)
\((\sqrt[n]{a})^k = \sqrt[n]{a^k}~~(a \neq 0~\textrm{si}~k < 0)~~(3)\)
\(\sqrt[n]{\sqrt[p]{a}} = \sqrt[np]{a}~~(4)\)
\(\sqrt[np]{a^p} = \sqrt[n]{a}~~(5)\)
Démonstration : Propriété 1
Soit \(x=\sqrt[n]{a}~\textrm{et}~y = \sqrt[n]{b},~~x~\textrm{et}~y\) sont donc des réels positifs, et on a \(x^n = a~\textrm{et}~y^n = b.\)
D'après les propriétés des exposants entiers, \(x^ny^n = (xy)^n = ab.\)
Le produit \(xy\) est positif, donc \(xy = \sqrt[n]{ab}.\)
Démonstration : Propriété 2
Soit et \(x = \sqrt[n]{a}~\textrm{et}~y = \sqrt[n]{b}\); le réel \(b\) étant non nul, il en est de même pour \(y.\)
Donc \(x \geq 0~\textrm{et}~y > 0.\)
D'après la définition de la racine \(n^{ieme}\) d'un réel, on a : \(x^n = a~\textrm{et}~y^n = b\)
D'où, en utilisant les propriétés des exposants entiers \((\frac{x}{y})^n = \frac{x^n}{y^n} = \frac{a}{b}.\)
De plus \(\frac{x}{y} \geq 0,\) donc \(\frac{x}{y} = \sqrt[n]{\frac{a}{b}}.\)
Démonstration : Propriété 3
Soit \(x = (\sqrt[n]{a})^k\) (\(x\) est un réel positif, non nul si \(k < 0\)).
D'après les propriétés des exposants entiers on a \(x^n = ((\sqrt[n]{a})^k)^n = (\sqrt[n]{a})^{kn} = ((\sqrt[n]{a})^n)^k.\)
D'où \(x^n = a^k,\) et \(x = \sqrt[n]{a^k}.\)
Démonstration : Propriété 4
Soit \(x = \sqrt[n]{\sqrt[p]{a}}\)(\(x\) est un réel positif).
On a donc \(x^n = \sqrt[p]{a},\) d'où \((x^n)^p = a.\)
Or, d'après les propriétés des exposants entiers \((x^n)^p = x^{np}.\)
D'où et \(x^{np} = a,\) et \(x \geq 0,\) par conséquent \(x = \sqrt[np]{a}.\)
Démonstration : Propriété 5
Soit \(x = \sqrt[np]{a^p}\) (\(x\) est un réel positif).
D'après la propriété (3), \((\sqrt[np]{a^p})^n = \sqrt[np]{a^{np}}.\)
D'où \(x^n = a\) et \(x \geq 0,\) par conséquent \(x = \sqrt[n]{a}.\)
Résolution dans \(\mathbb R\) de l'équation \(x^n = a, n\) étant un entier strictement positif
On appelle \((E)\) cette équation.
Si \((E)\) a une solution \(x\) alors nécessairement \(|x|^n = |a|,\) donc \(|x| = \sqrt[n]{|a|}\); cette équation a donc au plus deux solutions : \(\sqrt[n]{|a|}~\textrm{et}~-\sqrt[n]{|a|}.\)
Etudions le cas où \(n\) est pair : si \(a\) est positif on vérifie que les deux réels \(\sqrt[n]{a}~\textrm{et}~-\sqrt[n]{a}\) sont solutions de \((E),\) si \(a\) est strictement négatif \((E)\) n'a pas de solution car, dans le cas où \(n\) est pair, pour tout \(x\) réel \(x^n\)est positif.
Passons maintenant au cas où \(n\) est impair : dans ce cas pour tout \(x\) réel \(x^n\)a le même signe que \(x,\) donc si \(a\) est positif la seule possibilité est \(\sqrt[n]{a}\)et on vérifie que ce réel est bien solution de \((E),\) si \(a\) est strictement négatif, la seule possibilité est \(-\sqrt[n]{|a|} = -\sqrt[n]{-a}\)et on vérifie de même que c'est bien une solution de \((E).\)
En résumé on a :
Ensemble des solutions de l'équation \(x^n = a\):
Si n est pair :
\(\begin{cases} a \geq 0~~2~\textrm{solutions : }~\sqrt[n]{a}~\textrm{et}~-\sqrt[n]{a} \\ a < 0~~0~\textrm{solution}\end{cases}\)
Si n est impair :
\(\begin{cases}a \geq 0~~1~\textrm{solution : }\sqrt[n]{a} \\ a < 0~~1~\textrm{solution : }-\sqrt[n]{-a}\end{cases}\)
Remarque :
Dans le cas où \(n\) est impair l'équation a une solution unique pour tout réel \(a\) ce qui est en cohérence avec le fait que dans le cas où \(n\) est un entier naturel impair la fonction \(x \mapsto x^n\)est une bijection de \(\mathbb R\) sur \(\mathbb R\) (elle est continue strictement croissante sur \(\mathbb R\)).
On peut effectivement appliquer le théorème des fonctions réciproques à la fonction de \(\mathbb R\) dans \(\mathbb R~~x \mapsto x^{2p + 1}\), et définir sa fonction réciproque \(x \mapsto \sqrt[2p+1]{x}\)sur \(\mathbb R.\)
C'est ce que font certains auteurs, et il est fréquent de lire des expressions du type : \(\sqrt[3]{-8} = -2.\)
Ce n'est pas le choix qui a été fait ici, car cela peut conduire à des erreurs flagrantes si on fait les calculs sans précautions ; par exemple, on pourrait être étonné des résultats suivants :
\(\sqrt[3]{-8} = -2~\textrm{et}~\sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2\)
Mais en fait, la propriété \((5) \sqrt[np]{a^p} = \sqrt[n]{a}\) à laquelle on pense ici ne s'applique que pour \(a > 0\)ce qui n'est pas le cas de \(–8.\)
De plus, dès que l'on veut faire des opérations (somme, produit, composition...) entre les fonctions racines \(n^{ieme},\) il est nécessaire qu'elles soient toutes définies sur \(\mathbb R ^+\) et à valeurs dans \(\mathbb R ^+.\)