Etude de la fonction "puissance rationnelle"
Soit \(r\) un rationnel et \(\frac{p}{q}\)un représentant de \(r,~~(p, q)\) élément de \(\mathbb Z \times \mathbb N ^*.\)
D'après la définition, pour tout \(x\) réel positif \(x^r = x^{\tfrac{p}{q}} = \sqrt[q]{x^p} = (\sqrt[q]{x})^p\) \((x\) est supposé non nul si \(r< 0).\)
La fonction \(f_r : x \mapsto x^r\)apparaît donc comme la composée de \(f_p : x \mapsto x^p\) et de \(f_{\tfrac{1}{4}} : x \mapsto x^{\tfrac{1}{4}}\) dans un ordre quelconque, c'est-à-dire : \(f_r = f_{\tfrac{1}{4}} \circ f_p = f_p \circ f_{\tfrac{1}{4}}.\)
On va donc déduire l'étude de la fonction \(f_r : x \mapsto x^r\) de celles de \(f_p : x \mapsto x^p\) et \(f_{\tfrac{1}{4}} : x \mapsto x^{\tfrac{1}{4}} = \sqrt[q]{x}\) faites précédemment.
Pour tout entier \(q\) strictement positif, \(f_{\tfrac{1}{4}}\) est définie continue, strictement croissante sur \(\mathbb R ^+.\)
Pour tout entier \(p\) strictement positif, \(f_p\) est définie continue, strictement croissante sur \(\mathbb R ^+.\)
Pour tout entier \(p\) strictement négatif, \(f_p\) est définie continue, strictement décroissante sur \(\mathbb R ^{*+}.\)
Enfin si \(p\) est nul, on obtient la fonction constante \(x \mapsto 1\) définie sur \(\mathbb R ^{*+}.\)
On en déduit que
Si \(r > 0\)
La fonction \(f_r : x \mapsto x^r\) est définie, continue, strictement croissante sur \(\mathbb R ^+.\)
De plus \(\displaystyle \lim_{x \rightarrow +\infty}x^r = \displaystyle \lim_{x \rightarrow + \infty}(x^p)^{\tfrac{1}{4}} = +\infty.\)
Si \(r < 0\)
La fonction \(f_r : x \mapsto x^r\) est définie, continue, strictement décroissante sur \(\mathbb R^{*+}.\)
De plus \(\displaystyle \lim_{x \rightarrow + \infty}x^r = \displaystyle \lim_{x \rightarrow + \infty} (x^p)^{\tfrac{1}{q}} = 0~\textrm{et}~\displaystyle \lim_{x \rightarrow 0, x > 0}x^r = \displaystyle \lim_{x \rightarrow 0, x > 0}(x^p)^{\tfrac{1}{q}} = +\infty\)
La fonction\(f_r : x\mapsto x^r\) est dérivable sur \(R^{*+}\) comme composée de fonctions dérivables.
\(f_p' : x \mapsto px^{p-1}\)
\(f'_{\tfrac{1}{4}} : x \mapsto \frac{1}{q}x^{\tfrac{1}{q} - 1}\)
D'où \(f'_{\tfrac{p}{q}}(x) = f'_{\tfrac{1}{q}}(f_p(x))f'_p(x) = (\frac{1}{q}(x^p)^{\tfrac{1}{q} - 1})(px^{p-1}) = \frac{p}{q}x^{\tfrac{p}{q} - 1}.\)
La dérivée de \(x \mapsto x^r\) est donc \(x \mapsto rx^{r-1}\)
Ce qui généralise la formule trouvée pour les exposants entiers.
Remarque :
Dans le cas où \(r\) est strictement supérieur à \(1\) la fonction \(x \mapsto x^r\) admet une dérivée à droite en \(0,\) en effet \(\displaystyle \lim_{x\rightarrow 0, x> 0}\frac{x^r - 0}{x -0} = \displaystyle \lim_{x \rightarrow 0, x >0} x^{r-1} = 0.\)
La courbe représentative de la fonction \(x \mapsto x^r\)admet l'axe \(Ox\) comme demi tangente à l'origine.
Dans le cas où \(r\) est strictement compris entre \(0~\textrm{et}~1,\) la fonction \(x \mapsto x^r\) n'admet pas de dérivée à droite en \(0,\) en effet \(\displaystyle \lim_{x\rightarrow 0, x> 0}\frac{x^r - 0}{x -0} = \displaystyle \lim_{x \rightarrow 0, x >0} x^{r-1} = +\infty.\)
La courbe représentative admet alors l'axe \(Oy\) comme demi tangente à l'origine.
Compte tenu de l'étude précédente, on obtient les tableaux de variations suivants :
Cas où \(r > 0\)
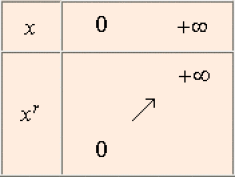
Cas où \(r < 0\)
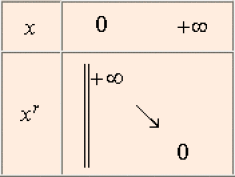
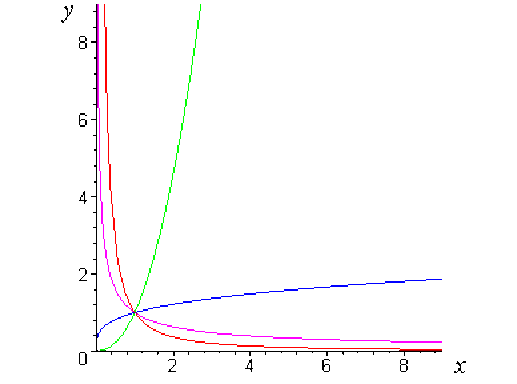
Voici, dans un repère orthonormé, quelques exemples de graphes :
\(\color{green} x \mapsto x^{\tfrac{11}{5}}\)
\(\color{blue} x \mapsto x^{\tfrac{2}{7}}\)
\(\color{magenta} x \mapsto x^{-\frac{2}{3}}\)
\(\color{red} x \mapsto x^{-\frac{13}{9}}\)
Remarque :
L'étude précédente montre que si \(r\) est non nul la fonction \(f_r : x \mapsto x^r\)est une bijection de \(\mathbb R^{*+}\) sur lui-même. Sa fonction réciproque est \(f_{\tfrac{1}{r}} : x \mapsto x ^{\tfrac{1}{r}}\); en effet, d'après les propriétés des exposants, on a pour tout réel strictement positif \(x,\) \((x^r)^{\tfrac{1}{r}} = (x^{\tfrac{1}{r}})^r = x^{\tfrac{r}{r}} = x.\)
C'est-à-dire \(f_{\tfrac{1}{r}} \circ f_r = f_r \circ f_{\tfrac{1}{r}} = Id_{\mathbb R ^{++}}.\)
Donc \(f_r^{-1} = f_{\tfrac{1}{r}}.\)