Fonction Arccosinus
Définition :
Soit \(f\) la restriction de la fonction cosinus à l'intervalle \([0, \pi].\)
\(f : [0, \pi] \rightarrow [-1, 1]\)
\(x \mapsto \cos x\)
La fonction \(f\) est continue et strictement décroissante sur l'intervalle \([0,\pi].\)
D'après le théorème dit " des fonctions réciproques " on peut affirmer que
\(f([0, \pi]) = [f(\pi), f(0)] = [-1, 1]\)
et que \(f\) établit une bijection de \([0, \pi]\) sur \([-1, 1].\)
La fonction réciproque de \(f\) est appelée Arccosinus et notée \(x \mapsto \arccos x.\) C'est une bijection de l'intervalle \([-1, 1]\)sur l'intervalle \([0, \pi].\)
\(\arccos : [-1, 1] \rightarrow [0, \pi]\)
\(x \mapsto \arccos x\)
Pour tout \(x\) de l'intervalle \([-1, 1],\) \(\arccos x\) est donc l'unique élément de l'intervalle \([0, \pi]\) qui a pour cosinus le réel \(x.\)
Remarque :
La notation \(y = \arccos x\)peut se lire : \("y\) est l'arc (de l'intervalle \([0, \pi])\) dont le cosinus vaut \(x"\)
Par définition
\(\boxed{\begin{cases} x \in [-1, 1] \\ y = \arccos x \end{cases} \Leftrightarrow \begin{cases} y \in [0, \pi] \\ \cos y = x \end{cases}}\)
Exemple :
\(\arccos \frac{1}{2} = \frac{\pi}{3}\)car \(\frac{\pi}{3} \in [0, \pi]\) et \(\cos \frac{\pi}{3} = \frac{1}{2}\)
Il y a une infinité de réels dont le cosinus est égal à \(\frac{1}{2}.\) Mais parmi ces réels, seul \(\frac{\pi}{3}\) appartient à l'intervalle \([0, \pi].\)
Conséquence de la définition
\(\boxed{\forall x \in [-1, 1]~~~~\cos(\arccos x) = x}\)
\(\boxed{\forall x \in [0, \pi]~~~~\arccos(\cos x) = x}\)
Remarque :
L'expression \(\cos(\arccos x)\) n'est définie que pour x appartenant à l'intervalle \([-1, 1].\) Par contre l'expression \(\arccos(\cos x)\) est définie pour tout réel \(x,\) mais l'égalité \(\arccos(\cos x) = x\) n'est vraie que pour \(x\) appartenant à l'intervalle \([0, \pi].\)
Par exemple, \(\arccos(\cos(-\frac{\pi}{3})) = \arccos(\cos(\frac{\pi}{3})) = \frac{\pi}{3}.\)
Propriété :
La fonction Arccosinus est continue et strictement décroissante sur \([-1, 1].\)
C'est une conséquence directe du théorème des fonctions réciproques.
\(\begin{array}{|c | c c c|}\hline x & -1 & & 1 \\ \hline & \pi& & \\ \arccos x & & \searrow & \\ & & & 0 \\ \hline \end{array}\)
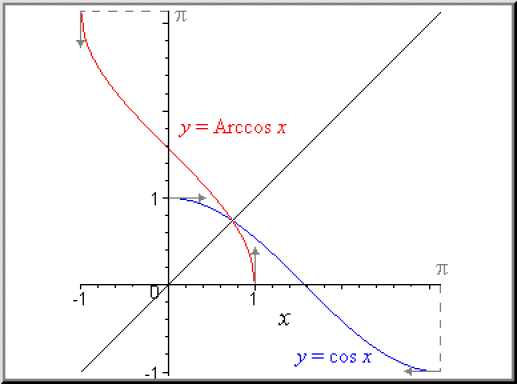
Graphe
Dans le plan rapporté à un repère orthonormé la courbe représentative de la fonction Arccosinus est la courbe symétrique par rapport à la première bissectrice de la courbe représentative de la restriction de cosinus à l'intervalle \([0, \pi].\)
Dérivée
La fonction \(f\) est dérivable sur \([0, \pi]\) et \(f'(x) = -\sin x.\)
La dérivée de \(f\) ne s'annule pas sur \(]0, \pi[,\)
la fonction Arccosinus est donc dérivable sur \(]-1, 1[\)et
\(\forall x \in ]-1, 1[~~~~(\arccos)'(x) = \frac{1}{f'(f^{-1}(x))} = -\frac{1}{\sin(\arccos(x)}.\)
Calcul de \(\sin(\arccos x)\) : \(\sin^2(\arccos x) = 1 - \cos^2(\arccos x) = 1 - x^2\)
et comme \(x\in]-1, 1[~~\arccos x \in ]0, \pi[,\) donc \(\sin(\arccos x) > 0.\) D'où
\(\boxed{\sin(\arccos x) = \sqrt{1 - x^2}}\)
On a donc
\(\boxed{\forall x \in ]-1, 1[~~~~(\arccos)'(x) = -\frac{1}{\sqrt{1 - x^2}}}\)
Attention :
La fonction Arccosinus est définie et continue sur l'intervalle fermé \([-1, 1]\)et dérivable sur l'intervalle ouvert \(]-1, 1[.\)