Fonction Arctangente
Définition :
Soit \(f\) la restriction de la fonction tangente à l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
\(f : ]-\frac{\pi}{2}, \frac{\pi}{2}[ \rightarrow \mathbb R\)
\(x \mapsto \tan x\)
La fonction \(f\) est continue et strictement croissante sur l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
D'après le théorème dit " des fonctions réciproques " on peut affirmer que
\(f(]-\frac{\pi}{2}, \frac{\pi}{2}[) = ]\displaystyle \lim_{x \rightarrow -\frac{\pi}{2}^+}f(x), \displaystyle \lim_{x \rightarrow \frac{\pi}{2}^-}f(x)[ = \mathbb R\)
et que \(f\) établit une bijection de \(]-\frac{\pi}{2}, \frac{\pi}{2}[\) sur \(\mathbb R.\)
La fonction réciproque de \(f\) est appelée Arctangente et notée \(x \mapsto \arctan x.\) C'est une bijection de \(\mathbb R\) sur l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
\(\arctan : \mathbb R \rightarrow ]-\frac{\pi}{2},\frac{\pi}{2}[\)
\(x \mapsto \arctan x\)
Pour tout réel \(x\) \(\arctan x\)est donc l'unique élément de l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[\)qui a pour tangente le réel \(x.\)
Remarque :
La notation \(y = \arctan x\)peut se lire : \("y\) est l'arc (de l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[)\) dont la tangente vaut \(x"\)
Par définition
\(\boxed{\begin{cases} x\in \mathbb R \\ y = \arctan x\end{cases} \Leftrightarrow \begin{cases} y \in ]-\frac{\pi}{2}, \frac{\pi}{2}[ \\ \tan y = x\end{cases}}\)
Exemple :
\(\arctan 1 = \frac{\pi}{4} \)car \(\frac{\pi}{4} \in ]-\frac{\pi}{2}, \frac{\pi}{2}[\)et \(\tan \frac{\pi}{4} = 1.\)
Attention :
\(\forall x \in \mathbb R,~~\tan x = 1\Leftrightarrow x = \frac{\pi}{4} + k\pi~~~~(k \in \mathbb Z)\)
Il y a une infinité de réels dont la tangente est égale à \(1.\) Mais parmi ces réels, seul \(\frac{\pi}{4}\)appartient à l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
Conséquence de la définition
\(\boxed{\forall x \in \mathbb R~~~~\tan(\arctan x) = x}\)
\(\boxed{\forall x \in ]-\frac{\pi}{2}, \frac{\pi}{2}[~~~~\arctan(\tan x) = x}\)
Remarque :
L'expression \(\arctan(\tan x)\) est définie pour tout réel \(x\) différent de \(\frac{\pi}{2} + k\pi~~(k \in \mathbb Z),\) mais l'égalité \(\arctan(\tan x) = x\) n'est vraie que pour \(x\) appartenant à l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
Par exemple, \(\arctan(\tan\frac{5\pi}{4} )= \arctan(1) = \frac{\pi}{4}.\)
Propriété : 1
La fonction Arctangente est continue et strictement croissante sur \(\mathbb R.\)
C'est une conséquence directe du théorème des fonctions réciproques.
\(\begin{array}{|c | c c c|}\hline x & -\infty & & +\infty \\ \hline & & & \frac{\pi}{2} \\ \arctan x & & \nearrow & \\ & -\frac{\pi}{2} & & \\ \hline \end{array}\)
Propriété : 2
La fonction Arctangente est impaire.
Démonstration : Propriété 2
L'ensemble de définition est \(\mathbb R\) donc centré en \(0.\)
Soit \(x \in \mathbb R\)et \(y = \arctan x\)on a alors \(\tan y = x\)et \(y \in ]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
La fonction \(\tan\) étant impaire, \(\tan(-y) = -x\)et \(-y \in ]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
D'où \(\arctan(-x) = -y = - \arctan x.\)
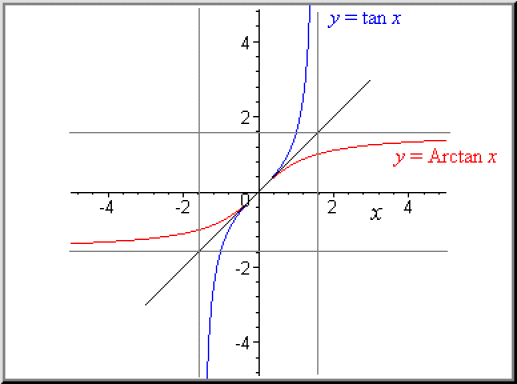
Graphe
Dans le plan rapporté à un repère orthonormé la courbe représentative de la fonction Arctangente est la courbe symétrique par rapport à la première bissectrice de la courbe représentative de la restriction de tangente à l'intervalle \(]-\frac{\pi}{2}, \frac{\pi}{2}[.\)
Dérivée
La fonction \(f\) est dérivable sur \(]-\frac{\pi}{2}, \frac{\pi}{2}[\) et \(f'(x) = 1 + \tan^2 x.\) La dérivée de \(f\) ne s'annule pas sur \(]-\frac{\pi}{2}, \frac{\pi}{2}[,\) la fonction Arctangente est donc dérivable sur \(\mathbb R\)
et \(\forall x \in \mathbb R~~~~(\arctan)'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{1 + \tan^2(\arctan x)} = \frac{1}{1 + x^2}.\)
On a donc
\(\boxed{\forall x \in \mathbb R~~~~(\arctan)'(x) = \frac{1}{1 + x^2}}\)