Introduction
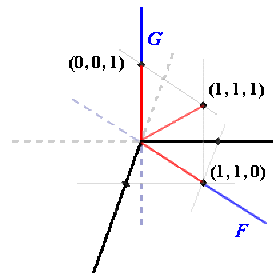
Dans \(\mathbb R^3\), soit \(F\) le sous espace vectoriel engendré par \((1,1,0)\) et \(G\) le sous-espace vectoriel engendré par \((0,0,1)\).
L'élément \((1,1,1) = (1,1,0) + (0,0,1)\) n'est ni dans \(F\), ni dans \(G\) :
\(F \cup G\) n'est pas stable pour l'addition.
Ce n'est pas un sous-espace vectoriel de \(\mathbb R^3\).
Dans \(\mathbb R^3\), soient les sous-espaces vectoriels \(F\) et \(G\) suivants :
\(F = \{ (x,y,z) \in \mathbb R^3 , x = y = z\}\)
\(G = \{ (x,y,z) \in \mathbb R^3 , x - y = 0 \}\)
Alors \(F\) est contenu dans \(G\), d'où \(F \cup G\) et \(F \cup G\) est un sous-espace vectoriel de \(\mathbb R^3\)

Donc dans un \(\mathbf K\textrm{-espace}\) vectoriel \(E\), la réunion \(F \cup G\) de deux sous-espaces vectoriels \(F\) et \(G\) peut être ou ne pas être un sous-espace vectoriel de \(E\).