Définition
Définition : Sous-espace non isotrope, sous-espace isotrope, sous-espace totalement isotrope
Soit \(E\) un \(\mathbf K\textrm{-espace}\) vectoriel, \(f\) une forme bilinéaire symétrique sur \(E\) et \(F\) un sous-espace vectoriel de \(E\).
Le sous-espace \(F\) est non isotrope pour \(f\) si le vecteur nul est le seul vecteur de \(F\) orthogonal à \(F\), c'est-à-dire si \(F\cap F^\perp=\{0_E\}\).
Le sous-espace \(F\) est isotrope pour \(f\) s'il existe un vecteur non nul de \(F\) qui est orthogonal à \(F\), c'est-à-dire si \(F\cap F^\perp \neq \{0_E\}\).
Le sous-espace \(F\) est totalement isotrope pour \(f\) si tous les vecteurs de \(F\) sont orthogonaux à \(F\), c'est-à-dire si \(F\cap F^\perp\).
Exemple :
Soit \(f\) la forme bilinéaire symétrique de \(\mathbf R^3\) définie pour tout \(x=(x_1,x_2,x_3),~y=(y_1,y_2,y_3)\) de \(\mathbf R^3\)par \(f(x,y)=x_1y_1+x_2y_2-x_3y_3\).
Le sous-espace \(F\) de \(\mathbf R^3\) d'équation \(x_1+x_2+x_3=0\) est non isotrope pour \(f\).
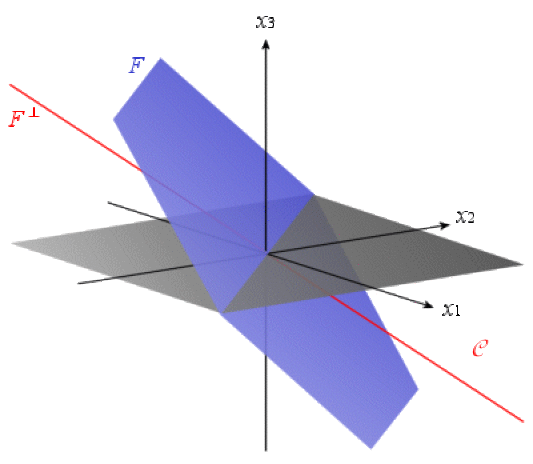
\(F :x_1+x_2+x_3=0\)
\(F^\perp=Vect\{(1,1,-1)\}\)
\(F\cap F^\perp=\{0_E\}\)
Le sous-espace \(G\) de \(\mathbf R^3\) d'équation \(x_1+x_3=0\) est isotrope pour \(f\).

\(G :x_1+x_3=0\)
\(G^\perp=Vect\{(1,0,-1)\}\)
\(G^\perp\subset G\)
Le sous-espace \(H\) de \(\mathbf R^3\) engendré par \(u=(1,0,1)\) est totalement isotrope pour \(f\).

\(H=Vect\{(1,0,1)\}\)
\(H^\perp :x_1-x_3=0\)
\(H\subset H^\perp\)
Exemple : Autres exemples
Soit \(f_1\) la forme bilinéaire symétrique de \(\mathbf R^3\) définie pour tout \(x=(x_1,x_2,x_3)\) et tout \(y=(y_1,y_2,y_3)\) de \(\mathbf R^3\) par \(f_1(x,y)=x_1y_1\).
Considérons \(F\) le sous-espace vectoriel de \(\mathbf R^3\) d'équation \(x_1+-x_2+x_3=0\). \(F\) étant engendré par les vecteurs \(u_=(1,-1,0)\) et \(v=(0,1,-1)\), le vecteur \(x=(x_1,x_2,x_3)\) appartient à \(F^\perp\) si et seulement si :
\(\left\{\begin{array}{l}f_1(x,u)=0 \\ f_1(x,v)=0 \end{array}\right.\Leftrightarrow\left\{\begin{array}{r}x_1=0\\0=0\end{array}\right.\)
On a donc \(F^\perp=\{(0,x_2,x_3)\in \mathbf R^3\}\) et \(F\cap F^\perp=\{(0,x_2,-x_2)\in \mathbf R^3\}\). Il existe des vecteurs de \(F\), autres que le vecteur nul, qui sont orthogonaux à tous les vecteurs de \(F\) pour \(f_1\): \(F\) est un sous-espace isotrope pour \(f_1\).
Considérons \(G\) le sous-espace vectoriel de \(\mathbf R^3\) engendré par le vecteur \(u'=(1,0,1)\). Le vecteur \(x=(x_1,x_2,x_3)\) appartient à \(G^\perp\) si et seulement si :
\(f_1(x,u')=0\Leftrightarrow x_1=0\)
On a donc \(G^\perp=\{(0,x_2,x_3)\in \mathbf R^3)\}\) et \(G\cap\ G^\perp=\{0_{\mathbf R^3}\}\). Le vecteur nul est le seul vecteur de \(G\) orthogonal à tous les vecteurs de \(G\) pour \(f_1\), \(G\) est un sous-espace non isotrope pour \(f_1\).
Considérons \(L\) le sous-espace vectoriel de \(\mathbf R^3\) d'équation \(x_1=0\). Si \(x=(x_1,x_2,x_3),y=(y_1,y_2,y_3)\) sont deux vecteurs de \(L\), on a \(x_1=y_1=0\) donc \(f_1(x,y)=0\). Ceci prouve que tout vecteur de \(L\) est orthogonal à \(L\) et \(L\) est un sous-espace totalement isotrope pour \(f_1\).
On peut vérifier que \(L\) est le cône isotrope de \(f_1\).
Remarques :
Dans l'exemple du cours où \(f\) est la forme bilinéaire non dégénérée sur \(\mathbf R^3\) définie par \(f(x,y)=x_1y_1+x_2y_2-x_3y_3\), \(F\) est un sous-espace non isotrope pour \(f\). Dans l'exemple ci-dessus \(f_1\) est une forme bilinéaire dégénérée sur \(\mathbf R^3\), \(F\) est un sous-espace isotrope pour \(f_1\).
Soit \(f_2\) la forme bilinéaire symétrique sur \(\mathbf R^3\) définie pour tout \(x=(x_1,x_2,x_3),~y=(y_1,y_2,y_3)\) de \(\mathbf R^3\) par \(f_2(x,y)=x_1y_1+x_2y_2+x_3y_3\).
Considérons \(F\) un sous-espace vectoriel (quelconque) de \(\mathbf R^3\) et \(x=(x_1,x_2,x_3)\) un vecteur de \(F\) orthogonal à tous les vecteurs de \(F\) pour \(f_2\). Ce vecteur est en particulier isotrope, par conséquent il vérifie \({x_1}^2+{x_2}^2+{x_3}^2=0\) et on a \(x_1=x_2=x_3=0\). Le vecteur nul est donc le seul vecteur de \(F\) orthogonal à tous les vecteurs de \(F\) et \(F\) est un sous-espace non isotrope pour \(f_2\).
Remarque :
Le sous-espace \(\{0_E\}\) n'est pas isotrope.
Si \(f\) est dégénérée, \(E\) est isotrope.
Un sous-espace totalement isotrope non réduit au vecteur nul est en particulier isotrope.
Soit \(E\) un \(\mathbf K\textrm{-espace}\) vectoriel et \(f\) une forme bilinéaire symétriques sur \(E\).
Si \(x\in E\) est un vecteur isotrope alors le sous-espace engendré par \(x\) est totalement isotrope.
Si \(F\) est sous-espace isotrope alors \(F^\perp\) est aussi un sous-espace isotrope. En effet si \(F\) est isotrope alors il existe un vecteur non nul \(x\in F\) orthogonal à \(F\), c'est-à-dire tel que \(x\in F\cap F^\perp\). Comme \(x\in F\), pour tout \(y\in F^\perp\) on a \(f(x,y)=0\). Cela signifie que le vecteur non nul \(x\) de \(F^\perp\) est orthogonal à \(F^\perp\): le sous-espace \(F^\perp\) est isotrope. (On peut établir ce résultat autrement en utilisant l'inclusion \(F\subset (F^\perp)^\perp\). On a \(F\cap F^\perp\subset F^\perp \cap(F^\perp)^\perp\), donc si \(F\) est sous-espace isotrope alors \(F^\perp\) est aussi un sous-espace isotrope).