Exemple
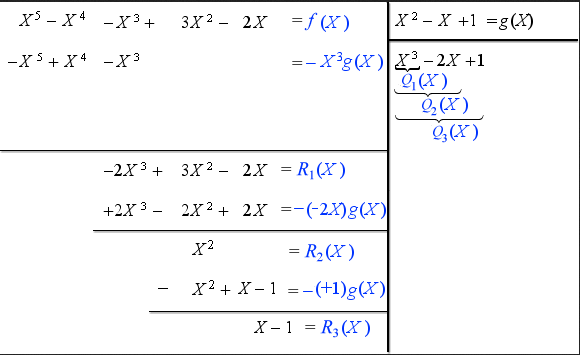
Les restes successifs \(R_1\) et \(R_2\) sont non nuls et chacun est de degré supérieur ou égal à celui de \(g\) qui est égal à 2. C'est pourquoi on continue la division.
Par contre \(R_3\) est un polynôme de degré 1, donc de degré strictement inférieur à celui de \(g\). La division est donc terminée : \(Q_3\) en est le quotient et \(R_3\)le reste. L'identité de la division euclidienne est donc : \(\begin{array}{ccccc}\underbrace{X^5-X^4-X^3+3X^2-2X}&=&\underbrace{(X^2-X+1)}&\underbrace{(X^3-2X+1)}&\underbrace{+X-1}\\f(X)&&g(X)&Q(X)&R(X)\end{array}\)
Description de l'algorithme pas à pas
\(f(X)=X^5-X^4-X^3+3X^2-2X\)
\(g(X)=X^2-X+1\)
\(Q_{partiel}(X)\) | \(Q(X)\) | R(X) |
0 | \(X^5-X^4-X^3+3X^2-2X=f(X)\) | |
\(X^3\) | \(X^3=Q_1(X)\) | \(-2X^3+3X^2-2X=R_1(X)\) |
\(-2X\) | \(X^3-2X=Q_2(X)\) | \(X^2=R_2(X)\) |
1 | \(X^3-2X+1=Q_3(X)\) | \(X-1=R_3(X)\) |